9161

Flat Earth Theory / Re: Polaris proves the earth is round.

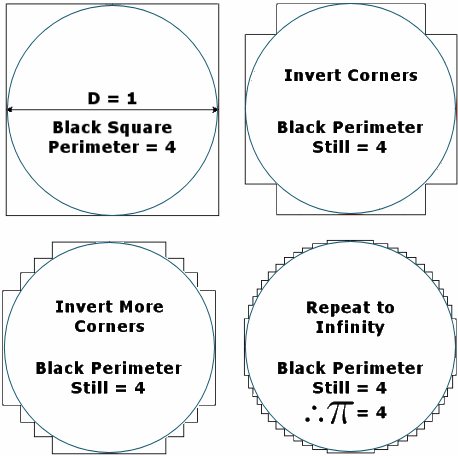
« on: February 18, 2016, 04:10:21 AM »

... so the 'real' circumference in nature will be longer than the perfect circle, and sometimes much longer than a perfect circle, because of all the imperfections made by nature, right? But then 'pi' would never be a constant (e.g. = 4) - it would just be bigger than 3,1415.

The most perfect circle possible in a quantized universe would have a pi of 4. Most other circles may have slightly different values for pi, as they are less perfect, but that is mostly irrelevant to the discussion since the continuous universe of the Ancient Greeks also ignores imperfect circles. Any opposing model to the standard ancient one would assume the most perfect circle possible as well when coming up with a value for pi.

I'm sorry, but this is just lame. We're talking about angles here, not "string theory ". Angles, like distances, are simply a way to quantify and/or describe the relationship physical objects have with one another in 3D space.
You say, "Samuel Birley Rowbotham teaches us in Earth Not a Globe that we must adopt our concept of perspective from real world experience and observations". It's terrific that you have such faith in the authority of your teacher, but he apparently has never really done much observing. You would do better to ask an architect, a navigator, a surveyor, or a cartographer, people who successfully use geometry everyday in real world observations. Applied mathematics like trigonometry were derived from pure observation and have been tried and tested for literally thousands of years. Trigonometry is not a theory. It works because it's true. Trigonometric relationships in the physical world are as certain as 2+2=4. They are as certain as any physical law. So if your flat earth sun does not obey physical laws then it cannot be physical and so you need to stop pretending that Flat Earth Theory is not a religion, because that's exactly what you are saying.

Why are you trying to use unverified ancient geometry/trigonometry as a proof of anything?

The Ancient Greeks did not verify that circles actually exist, and they did not verify that perspective lines actually stretch into infinity as they theorized.

Exactly.  Zetetics claim to hold observation over theory, but then this nonsense about plancks, and PI = 4?  Take a look around your home (AKA "conduct an observation").  Find an object that the rest of us would call 'round' and look at it.  Does it appear to be round?  If so, then the same philosophy that makes you say "The world LOOKS flat, I guess it must BE flat" should also lead you to the conclusion "This object LOOKS like a circle, I guess it must BE a circle".  Wrap a string around the can, measure its length.  "The strings MEASURES as if it were about 3.14 times the diameter, I guess it must BE 3.14 times the diameter."  Repeat for other round objects.  "Every round I object I MEASURE has a perimeter of 3.14 times its diameter, I guess ALL round objects exhibit that relationship"

When I pick up a can it looks like an object. It looks like a shape of some sort. I can safely say that it is an object. Assigning words like "circle" or "cylinder" to that shape brings me into the continuous universe of the Ancient Greeks, which we are increasingly coming to find were full of baloney, and whose science can be disproven by a simple act of walking through a door.

9162

Flat Earth Theory / Re: Polaris proves the earth is round.

« on: February 17, 2016, 06:27:15 AM »

So I just measured the circumference and diameter of a circular can on my desk and obtained C = 167 mm, D = 53 mm.
Is this then not reality!??

No, you drew a line through zig zags and came up with a figure that does not reflect reality.

9163

Flat Earth Theory / Re: Sun and Moon shape

« on: February 17, 2016, 01:40:54 AM »

You apparently have not bothered to read any of our material.

You apparently have not bothered to debate my point.
Instead you point to the vast material which
- contradicts itself
- makes too many assumptions
- does not grasp the basics of geometry, gravity, physics, maths, chemistry or anything else that may disprove your theory
- varies from one person to the next
- assumes that the region below the equator line cannot exist

Please answer the questions or admit that you cannot.

Still waiting...

Please keep the discussion related to the topic.

9164

Flat Earth Theory / Re: Polaris proves the earth is round.

« on: February 17, 2016, 01:24:11 AM »

It's not off topic. It is important for the topic to understand that the Geometry of the Ancient Greeks is simply wrong, and does not reflect reality. Zeno’s paradox alone leads to the conclusion that space is quantized, and therefore circles do not exist and pi is not 3.14159...

We see from experiment that we are able to walk through doors, and therefore we must design our science to make it possible to walk through doors, and not imagine some hypothetical construct imaging space and time as continuous. We must design our science from the observed and experienced, not idealistic theories.

I just got back from taking my dog for a walk.  Not only did I make it 1/2 way I made it to the end of the park and back to my boat.

During this walk my dog was able to catch up to me after lagging behind to smell different things.  Reason being I was moving slower than her.

I threw a ball for her to chase and it traveled away from me and landed on the grass.

All observed and experienced by me.

Are you sure that the Zeno's paradoxes are not just thought experiments/exercises? 

I am just asking since my experiences walking my dog surely seemed like reality. 

Zeno's paradoxes are scathing criticisms of the theory that space and time are continuous. Since you were able to do all of those things, it is a proof that space and time is discrete.

Just like when I use 3.14 to determine things like the circumference of a circle and the answer being correct.

It's correct in the mathematical fantasy of the Ancient Greeks. Incorrect in reality.

9165

Flat Earth Theory / Re: Polaris proves the earth is round.

« on: February 16, 2016, 10:29:45 PM »

It's not off topic. It is important for the topic to understand that the Geometry of the Ancient Greeks is simply wrong, and does not reflect reality. Zeno’s paradox alone leads to the conclusion that space is quantized, and therefore circles do not exist and pi is not 3.14159...

We see from experiment that we are able to walk through doors, and therefore we must design our science to make it possible to walk through doors, and not imagine some hypothetical construct imaging space and time as continuous. We must design our science from the observed and experienced, not idealistic theories.

9166

Flat Earth Theory / Re: Polaris proves the earth is round.

« on: February 16, 2016, 09:26:24 PM »

also, why do you believe that space is discrete and not continuous?  i think "it absolutely makes more sense to base science off of the observed and experienced rather than the theoretical and hypothetical," and there is no direct experimental evidence to suggest that space is discrete.  i also don't get why you're more interested in the results of your thought experiment than you are with observed and experienced measurements of pi.  you're being extremely pedantic.

There is experimental evidence. Space and time can be demonstrated to be quantized by simply walking from one end of your room through a door at the other end.

See: http://barang.sg/index.php?view=achilles&part=8

8. Is space quantized?

Men have long wondered if matter is infinitely divisible. For example, can you keep halving a piece of wood forever to obtain ever tinier pieces of wood? Nowadays, we know that the answer is no. Matter is atomic in nature and not infinitely divisible.

Surprisingly, the same question may be asked of space. (Not to mention time.)

Thus, when Zeno edges his points ever closer to the doorway, he tacitly assumes that the distance between a point and the doorway may be as small as one likes. This is to assume that space is infinitely divisible.



But if space, like matter, is atomic in nature, there will actually be a smallest distance beyond which we can divide space no further, as it were. And so there will be a limit to how close Zeno’s points can approach the doorway, meaning that his sequence of points must eventually come to a halt!

We can illustrate this concretely because contemporary physicists actually believe that space is atomic in nature, or quantized, as they like to say. (From the Latin term quantum, meaning amount.)

Thus, the “Planck length,” named after the German physicist Max Planck, is supposed to be the smallest quantum of length permitted by nature, so far as physicists know.

The underlying physics does not matter here (it has nothing to do with a tortoise), but the Planck length is about 1.6 × 10-35 m, which is a miniscule distance indeed. Roughly speaking, it stands to an atom as an atom stands to the sun!

Let’s work with this number and see what happens.

Consider our table from before, where some relevant lines have been added. Notice that once Achilles reaches point 117, his distance to the doorway has become shorter than the Planck length.

Point     Meters to doorway
1     1
2     1/2
3     1/4
.
.
.     .
.
.
116     2.4 × 10^-35
117     1.2 × 10^-35
.
.
.     .
.
.

But if the physicists are right, this distance is too short to be of spatial significance. This means that we cannot regard point 117 and the doorway as being two separate locations. Given the atomic nature of space, these locations must be regarded as being one and the same.

So the last point that Zeno can really lay down is point 116. And once Achilles reaches it, his next motion takes him to the doorway because there is no other location “in between” for him to occupy.

This sounds incredible, but if space is quantized, that is how it is.

Now, on the solution being considered, space must be quantized in this way because, as explained previously, Zeno’s sequence must contain a last point if Achilles is to “escape” to the doorway, and quantizing space seems to be the only way to ensure this. So even if the physicists had not yet discovered it, Zeno’s paradox already reveals the atomic nature of space.

Likewise, no pie can be infinitely sliced in the manner shown before because, beyond a certain point, the slices will be too thin to be spatially distinguishable and no further “slicing” can meaningfully occur.

This diagnosis, if correct, would be truly remarkable. It’s one thing to believe that space is quantized on detailed experimental grounds (like modern physicists), but quite another to deduce it simply by reflecting on whether a man can reach a doorway!

Does Zeno’s paradox really show that space must be quantized in this way?

Well, it really depends on the considerations of the previous section. In particular, is it really true that Achilles cannot reach the doorway unless Zeno’s sequence contains a last point for him to cross?

To answer this question, we must sharpen those considerations a little further. And we can do this by considering an unusual device known as Thomson’s lamp.

If you can make it through the door, it is a proof that space is quantized.

but let's assume that it is.  how would you go about "tracing a line" along all of the little pixelated plancks?  more importantly, with what would you trace the line?  wouldn't you have to make it with something also made out of little pixels?  i don't know how to express this notion mathematically, but you can't unfold the little pixels into a line to measure their "length" in this manner.  it's very similar to what i said above about how the perimeter of the square in your proof is never going to 'unfold' into a straight line, so it doesn't actually approximate the circle's diameter.  you can't 'unfold' the perimeter of a planck unit.

here's a visual to try to get across what i'm saying in case i'm being unclear.


you're thinking of a pixelated circle like the image on the left, as if we could measure planck lengths with an even tinier piece of string or measuring tape or something.  but if planck lengths are the smallest length, then we can't measure them with units smaller than planck lengths.  the thing we use to measure the perimeter is also made of planck lengths and cannot be further subdivided, as on the right side.

i think maybe what i'm trying to get across is that you're thinking of a circle too much in terms of its circumference, and a circle should be thought of in terms of radius.  it's the shape with a constant radius; or, it's the shape for which every point on its perimeter is equidistant from the center.  making circle pixelated instead of continuous doesn't change anything.  the definition of a pxelated circle would then be something like the shape for which each point on the perimeter is as equidistant as possible from the center.  if you make such a shape, and if count the number of pixels composing the perimeter and the diameter, you'll get a ratio very close to 3.14159..., not 4.  the only possible way to get 4 is to measure your discontinuous/pixelated circle with a continuous line; in other words, to subdivide the space that you're defining as indivisible.  bad methodology.

I see in the image on the right that you were able to trace plancks with other plancks to create a perimeter to identify the boundaries of a shape. No subdivision of space was required.

9167

Flat Earth Theory / Re: Polaris proves the earth is round.

« on: February 16, 2016, 09:19:46 PM »

"so much of the perimeter curled up at the edges", is it?  If it's true of my circle, it's also true of your square.  Those four "straight" lines you used to box in the circle?  They are all kinds of jagged and crooked too, making each an unknown distance greater than the theoretical unit length.  They might not even be equal lengths, for all we know.  In fact, they could be infinitely long.  We cannot know the true length of anything, including your collapsing corners box, and thus all geometry and trigonometry is useless.

Except...we know that in the real, physical world, geometry and trig are the opposite of useless.  We know through experiments and observation that the objects we agree to call "circles" have a perimeter that measures 3.14159...... times the measured diameter of those objects.  We use that number to calculate how much sheet metal it will take, when rolled into a cylinder, to create a drum of a desired diameter, and viola!  The drum thus formed does indeed have the desired diameter!  We use the same 3.14159..... times radius times radius to calculate how much area is enclosed by these objects we agree to call "circles" and when we check with (for example) liquid in a drum, guess what?  There is as much liquid in the drum as the math said there would be!  Whereas, if you take 4 as your value of Pi nd calculate the amount of sheet metal to use for a given diameter drum, when you build it your drum will have a diameter larger than you wanted. 
BECAUSE PI ISN'T 4!! 
Then when you do your volume calculation with the actual diameter and Pi=4, you will find your drum cannot hold the amount you calculated. 
BECAUSE PI STILL ISN'T 4!!!

Again, Area = Perimeter * Radius * Radius only works for a circle. Only a circle has the necessary uniform shape for that equation to work. It does not work for a square, a triangle, or a complex polygon that looks like a circle.

Didn't you do these very tests when you were a child in school?  In my class we each were given a different length piece of construction paper.  We measured its length, formed it into a circle by taping the ends, then measured its diameter.  The whole class then reported their numbers, which the teacher wrote on the board.  She then calculated the ratios, to demonstrate that every circle had the same ratio (give or take the measuring skill of children of course).  We then filled the cylinders with a single layer of peas, and counted them as a rough measure of area.  Again the numbers were called out to teacher, who applied Pi R squared to prove the rule, again subject to the imperfection of school children's construction.

That test is inaccurate, as you are not actually measuring the imperfections of the circumference. You are laying waypoints on a map to get a distance without considering the mountains.

9168

Flat Earth Theory / Re: Polaris proves the earth is round.

« on: February 16, 2016, 12:23:56 AM »

well, even a jagged not-perfect circle does in fact follow the calculations of Pi to enough decimal places to be accurate enough to satisfy the needs of engineering, science, and math.

Just look at the equation. Area = pi * radius * radius. It's assuming that the area is directly connected to the perimeter times the radius squared. You can't do that with a polygon.

Most of the additional length of the perimeter in the very pixilated circle in my example is in the very small steps at the edge of the circle, and does not add significant area to the whole of the object. Using that area equation just doesn't work, as it is a highly complex polygon and not a circle. The area of the object is obviously not the perimeter times the radius squared when much of the perimeter is so curled up at the edges like that.

9169

Flat Earth Theory / Re: Polaris proves the earth is round.

« on: February 15, 2016, 11:44:33 PM »

Wow.  So you think the whole world has been underestimating the circumference and area of every circle ever, by about 25 percent?  That the dimensions of a 55 gallon drum, calculated based on 3.14159, are wrong?  It actually contains closer to 70 gallons, but nobody in a very money-driven industry has noticed they are shipping more oil than they thought?

Using pi to calculate area does not make any sense if the shape is a polygon, since unlike a circle, the perimeter of a polygon is not related to its area.
Please refer to my example above of a triangle and a square with identical perimeters having different interior areas.

I fail to see any polygon mentioned in the post you were answering!
In Australia these drums are 44 (imperial) gallons and are cylindrical, so π would be very relevant.

So I can't make sense of your statement "Using pi to calculate area does not make any sense if the shape is a polygon"!

The difference in area would be minuscule if you treated the cylinder as a perfect circle where pi = 3.14159.. or a really really pixilated circle one where pi = 4.

In calculating the area of a polygon, you cannot use A= pi * r^2 , as polygons do not have areas that are directly related to their perimeter. See the square vs triangle example. Polygons are not uniform shapes like circles are. The equation assumes a shape where perimeter is directly related to area.

9170

Flat Earth Theory / Re: Polaris proves the earth is round.

« on: February 15, 2016, 12:15:17 AM »

Wow.  So you think the whole world has been underestimating the circumference and area of every circle ever, by about 25 percent?  That the dimensions of a 55 gallon drum, calculated based on 3.14159, are wrong?  It actually contains closer to 70 gallons, but nobody in a very money-driven industry has noticed they are shipping more oil than they thought?

Using pi to calculate area does not make any sense if the shape is a polygon, since unlike a circle, the perimeter of a polygon is not related to its area.

Please refer to my example above of a triangle and a square with identical perimeters having different interior areas.

9171

Flat Earth Theory / Re: Polaris proves the earth is round.

« on: February 13, 2016, 06:29:27 AM »

Exactly Tom! That's why I choose an orange - because it's not perfectly round. I'll have water to fill up all of it's 'imperfections' so I can measure it's 'real' volume, and thereby estimate pi (which will be larger than 3,1415xx because of the orange's imperfections).
What's wrong with the experiment?

Well, it's really the same experiment Daguerrohype is proposing. He seems to think that two shapes with the same perimeter should have the same total area within those shapes. He is wrong. I brought up the example of a triangle and a square with the same perimeters having different total areas within those shapes.

Referring to Daguerrohype, you say "He seems to think that two shapes with the same perimeter should have the same total area within those shapes." His actual statement was:

If we compare the area of a circle of radius 10 cm using both pi = 3.142 (to three decimal places) and pi = 4.000
10 x 10 x 3.142 = 314.2 cm^2
10 x 10 x 4.000 = 400.0 cm^2
The difference is an area of 85.8 cm^2.
I cannot visualise a circle with radius 10 cm and area 400 cm^2. If anyone can draw one, then please do. It might be useful to compare it (to scale) with a square of side length 20cm, as they have the same area.

Where he said that if we use the correct (to 3 places) value of π=3.142, we get the area of 314.2 cm² but if we take π=4.000, we get of 400.0 cm².

From what I can see what Daguerrohype actually says is quite correct. The circle and square only have the same perimeter and area if YOU insist on using YOUR stupid value of π=4. The sooner you can forget this "matter of definition" the better for everybody!

As I have tried to point out your so called proof is completely fallacious.
It's not a matter of definitions or maths it is simply wrong!

I was referring to this statement:

Thanks Tom, now if you can show the most refined "circle" next to a square with side length 2 x radius [edited], we can see whether they have the same area.

In fact if you can (apologies, I cannot), overlay the two figures to show the difference in area. I wager the "circle" will fit inside the square with room to spare.

If that is the case, then where is the missing area from the "circle"? Very well hidden indeed!

This doesn't really make sense, since the interior area within different shapes of the same perimeter are not related.

As far as the statement you quoted, an attempt to calculate the area of a circle using A = pi*r^2 with 4 in the place of pi, the error in the logic is that circles do not exist. You can't use traditional circle math to calculate that. The shape is not a circle, and the correct way to calculate the area is to use a method of calculating the area within a polygon.

9172

Flat Earth Theory / Re: Polaris proves the earth is round.

« on: February 13, 2016, 05:58:13 AM »

you're not wrong that the c/d ratio of real, physical circles is not pi.  pi isn't a real constant.

you're very wrong that this means that pi is a constant and that that constant is 4.  you're wronger to imply that 4 is a better approximation of c/d for real circles than pi.  your 'proof' is even more wronger. the 'crinkled up' perimeter of the square is never going to actually 'straighten' up in a way that gets closer and closer to the perimeter of the circle.  no matter how much you zoom in, it will never appear to approximate the perimeter of a circle.  if you were to keep zooming in on the circle's perimeter, you'll only ever see this, no matter how much you zoom in:


except it wouldn't look so shitty since i presume nature to be way better at ms paint than i am.

That's not really my point. My point is that there is no such thing as a circle in the universe. So therefore pi != 3.14159...

How would YOU best estimate the volume of e.g. an orange?

We could do the water experiment to get the volume. But the way you used it as a proof is irrelevant. Different shapes with the same perimeter don't all have the same interior area.

9173

Flat Earth Theory / Re: Polaris proves the earth is round.

« on: February 12, 2016, 06:42:18 PM »

Exactly Tom! That's why I choose an orange - because it's not perfectly round. I'll have water to fill up all of it's 'imperfections' so I can measure it's 'real' volume, and thereby estimate pi (which will be larger than 3,1415xx because of the orange's imperfections).

What's wrong with the experiment?

Well, it's really the same experiment Daguerrohype is proposing. He seems to think that two shapes with the same parameter should have the same total area within those shapes. He is wrong. I brought up the example of a triangle and a square with the same parameter having different total areas within those shapes.

How would YOU best estimate the volume of e.g. an orange?

Your experiment is irrelevant. Surface area is not related to interior area in any meaningful with polygons. See the square vs triangle with identical perimeter example above.

9174

Flat Earth Theory / Re: Polaris proves the earth is round.

« on: February 12, 2016, 06:13:58 PM »

Exactly Tom! That's why I choose an orange - because it's not perfectly round. I'll have water to fill up all of it's 'imperfections' so I can measure it's 'real' volume, and thereby estimate pi (which will be larger than 3,1415xx because of the orange's imperfections).

What's wrong with the experiment?

Well, it's really the same experiment Daguerrohype is proposing. He seems to think that two shapes with the same perimeter should have the same total area within those shapes. He is wrong. I brought up the example of a triangle and a square with the same perimeters having different total areas within those shapes.

9175

Flat Earth Theory / Re: Polaris proves the earth is round.

« on: February 12, 2016, 10:08:36 AM »

I'm talking about area, not circumference.

The area of the "circle" you describe with radius "r" is significantly less than the area of a square with side length "2r".

I raised this issue re the value of pi being constant. If pi is the same value for all calculations, the calculation of the area of a circle demonstrates that it cannot be 4.

Why would to total area within the two shapes need to be the same?

Would the total area within a square and a triangle need to be the same if they have an identical perimeter?

9176

Flat Earth Theory / Re: Polaris proves the earth is round.

« on: February 12, 2016, 09:46:15 AM »

Thanks Tom, now if you can show the most refined "circle" next to a square with side length 2 x diameter, we can see whether they have the same area.

In fact if you can (apologies, I cannot), overlay the two figures to show the difference in area. I wager the "circle" will fit inside the square with room to spare.

If that is the case, then where is the missing area from the "circle"? Very well hidden indeed!

Your logic needs a little work.

It is possible to draw a snake curled up inside of a square, with the length of that snake being longer than the circumference of the square it exists within.

A circle which contains curls of hidden area can easily fit in a square with the same circumference/perimiter.

9177

Flat Earth Theory / Re: Polaris proves the earth is round.

« on: February 12, 2016, 09:18:33 AM »

It absolutely makes more sense to base science off of the observed and experienced rather than the theoretical and hypothetical. What was provided was a model based on little more than an idea of how things should work under the theories of art school perspective and geometry, not how they actually work.

The Ancient Greeks made a lot of assumptions about the physical world when coming up with Geometry. A lot of the assumptions turned out to be mistakes. For one, circles do not actually exist, since the universe is quantized, and any such related math is inaccurate. If one were to trace a line along all of the little pixilated plancks which make up the circumference of the most perfect "circle" in the universe one would find that pi is actually equal to 4, rather than the theoretical value of 3.14159...

I will be writing more on this topic of experience vs hypothesis in The 21st Century Edition of Earth Not a Globe, a modernized reboot of Earth Not a Globe by Samuel Birley Rowbotham, which we are working on in the Earth Not a Globe Workshop.

Interesting thoughts about the differences between the physical and the theoretical world. I'll try to make this small experiment: I'll estimate the volume of an orange using pi= 4 or pi=3,1415, and then I'll submerge in water and see how much water it'll displace and compare the measured volume with the calculated ones. Does that make sense?

That would assume the orange is perfectly round. It is not.

BTW I measure (with a tape measure) th circumference of a metal lid of diameter 111.4 mm and it comes to 351 mm. When I divide that out I get a 3.15 - (can't get 4 out of it) I'll take those Greeks over the rubbish Mathis puts out any day!

You are assuming the circumference of a metal lid is perfectly round. It is not. If you were to actually trace in all of the imperfections of the circumference there would be additional length there.

If one were to trace a line along all of the little pixilated plancks which make up the circumference of the most perfect "circle" in the universe one would find that pi is actually equal to 4, rather than the theoretical value of 3.14159...

In addition to being used to calculate the circumference of a circle, pi is also used to calculate the area of the same shape. In order for pi to be of use in calculations, its value needs to remain constant. Disagree with that if you will.

If we compare the area of a circle of radius 10 cm using both pi = 3.142 (to three decimal places) and pi = 4.000

10 x 10 x 3.142 = 314.2 cm^2

10 x 10 x 4.000 = 400.0 cm^2

The difference is an area of 85.8 cm^2.

I cannot visualise a circle with radius 10 cm and area 400 cm^2. If anyone can draw one, then please do. It might be useful to compare it (to scale) with a square of side length 20cm, as they have the same area.

There is hidden area in the circumference of a non-perfect circle.

9178

Flat Earth Theory / Re: Polaris proves the earth is round.

« on: February 12, 2016, 05:33:41 AM »

It absolutely makes more sense to base science off of the observed and experienced rather than the theoretical and hypothetical. What was provided was a model based on little more than an idea of how things should work under the theories of art school perspective and geometry, not how they actually work.

The Ancient Greeks made a lot of assumptions about the physical world when coming up with Geometry. A lot of the assumptions turned out to be mistakes. For one, circles do not actually exist, since the universe is quantized, and any such related math is inaccurate. If one were to trace a line along all of the little pixilated plancks which make up the circumference of the most perfect "circle" in the universe one would find that pi is actually equal to 4, rather than the theoretical value of 3.14159...

I will be writing more on this topic of experience vs hypothesis in The 21st Century Edition of Earth Not a Globe, a modernized reboot of Earth Not a Globe by Samuel Birley Rowbotham, which we are working on in the Earth Not a Globe Workshop.

9179

Flat Earth Theory / Re: Polaris proves the earth is round.

« on: February 11, 2016, 05:00:14 PM »

This is pure nonsense. The illustration I posted is to scale. The angles and distances are right there in front of you. I'll post it again below. Notice that the distance needed to see a change in altitude from 20° to 10° (9,040 miles) is greater than the distance needed for polaris to drop from 90° to 20° (8,557 miles). If the diagram were to continue, the distance needed for Polaris to drop from 10° to 5° is more than the distance needed for it to drop from 90° to 10°, about 17,835 miles (a total of 35,433 miles from 90° to 5°). To see Polaris at 0°, the distance needed is infinity.

It would therefore be impossible to see the apparent altitude of any celestial object drop at a constant rate due to perspective if it was moving away at a constant speed. You can draw it out and measure the angles for yourself if you like, or just use an online right triangle calculator.
Triangles don't lie.

Under traditional perspective it is also impossible for the sun to ever set. However, Samuel Birley Rowbotham teaches us in Earth Not a Globe that we must adopt our concept of perspective from real world experience and observations, not some mathematical concept.

9180

Flat Earth Community / Re: Magnetic Field Line Diagram Help

« on: February 11, 2016, 08:39:05 AM »

That is a decent image, thank you. I really like the positioning of the field lines.

If I had any suggestions, they would be as follows:

1. Perhaps make the field lines thinner

2. Try either a teal or orange color for the lines

3. Maybe try a version which is not transparent, and we can just see the field line coming out of the earth on top. Lets see how that would look.