I've been stumbling over this, thought I'd figured it out, but now I'm back to confused.
I know how to calculate an
approximate distance to a visual (and a radar) horizon on a globe earth if accounting for atmospheric effects.
What I don't know is how to interpret Rowbotham's explanation for horizon and horizon phenomenon in a way to calculate or even estimate a distance to a horizon plane.
There are diagrams in Earth Not a Globe like this:

...where the ground plane appears to slope upward to eye-level and then level off.

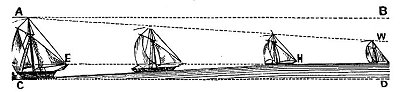
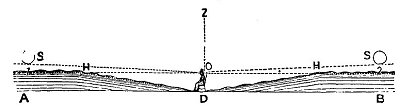
That point of H, where the slope changes from rising to level, parallel (coincident) with the level plane of the eye, is what EnaG claims is the horizon. I understand that. I even understand the explanation for why things further away than H can still be seen since H isn't a vanishing point. It's a line that is the edge of a plane, beyond which more distant things can still be seen (though smaller and smaller and ultimately converging with that edge (unless obscured by atmosphere or other other reasons first).
But what I can't grasp is how to figure where H is away from the observer. Tom Bishop might have misspoken when he wrote, "The horizon is one of the the furthest thing on earth that can be measured," but that has stuck with me and I've tried to work it out for myself, reading and re-reading the pertinent sections of EnaG. I'm just not getting it.
H is obviously dependent on the height of the viewer's eyes (or camera lens), as is true for a globe earth. But I can use geometry/trigonometry to calculate where the non-level eye line of the observer is tangent to the convex surface of the globe. And I can make adjustments or figure ranges of the distance to H to account for refractions. I can do all that on a globe.
What I can't resolve is how to do that given the conventional explanation for H in a flat earth model, where perspective plays such an important role.
I thought maybe Rowbotham's H might be calculated from the claimed limit of angular resolution of the human eye being 1 arcminute. But that's working out to be some crazy numbers, never witnessed or recorded. Diagrams and explanations and analogies are fine for conveying the concept, and I think I grasp the concept of what the horizon is for flat earth. But is there a way to figure how far away a horizon is in a flat earth model for a given height of the observer?
Basically, when do you know you are seeing a "true horizon" and, given that, how far away is it?