Reference #1
http://davidpratt.info/pyramid.htmFor example, the angle of slope of the Pyramid’s outer casing was 51.85 degrees.
Reference #2
The Pyramid Age, E.J. Sweeney
Chapter 1, page 4
This ratio provides a slope of 51.85 degrees (calculated).
Reference #3
http://stochasticprojectmanagement.com/?p=105ratio of height to width: 1.571 (one half of pi) slope: 51.85 degrees
Reference #4
http://www.numberscience.me.uk/Giza.htmlThe slant angle of the face of the pyramid approximates to 51.85 degrees.
Then, you have a huge problem.
The angle of the slope of the Pyramid’s outer casing is 51.85 degrees.
However, in order to reach/know this value, the architects of the Gizeh Pyramid must have had at their disposal the extended arctangent series:
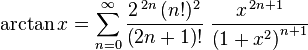
The VALUE of Tan 51.8554 degrees = the VALUE of two sacred cubits.
The projection on the granite leaf has some two decimal points accuracy, at best: 0.636 meters in length.
However, in 1985 the true height of the Gizeh pyramid was calculated to THE CENTIMETER:

Each one of those circles has a radius of 60 sacred cubits, to the centimeter.
One sacred cubit = 2/π or 7/22, as needed.
Here is the problem you have to solve.
TAN
X = 1.27330478216 = 0.636652 x 2
In order to build the pyramid you need the slope angle to at least two decimal places accuracy.
There is no other way to calculate the inverse tangent function of a certain angle (without using a pocket calculator/computer) other than resorting to power series, that is, utilizing calculus. Moreover, one would need a clear understanding of the concept of the radian measure.
The architects of the Giza Pyramid had these choices at their disposal in order to solve the following equation:
TAN X = 1.27330478216 = 0.636652 x 21. Maclaurin series in conjunction with the arctan reciprocal formula


(equation #3)
51.8554° = 0.907045 radians
1/1.27330478216 = 0.78535
Substituting the value of 0.78535 in the Maclaurin arctan series and solving the reciprocal arctan equation, up to the O(x
11) term we get:
0.905045
This corresponds to a 51.983° value.
Therefore, the builders of the Pyramid must have had at their disposal the notion of the derivative (either the Newton-Leibniz or the Madhava definitions) in order to obtain the arctan Maclaurin series, not to mention the reciprocal arctan equation; even in that case, they had to be able to compute powers of certain numbers, going perhaps all the way to the O(x
17) term (in the Maclaurin series) or even beyond, to obtain a meaningful accuracy.
2. Extended arctangent series
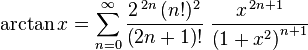
This is a result from advanced calculus.
3. Gauss-Pfaff-Borchardt-Carlson iterative formula
http://www.ams.org/journals/mcom/1972-26-118/S0025-5718-1972-0307438-2/S0025-5718-1972-0307438-2.pdfThis formula necessitates the use of the concept of derivatives for its mathematical proof.
https://books.google.ro/books?id=cGnSMGSE5Y4C&pg=PR20&lpg=PR20&dq=numerical+methods+that+work+forman+acton&source=bl&ots=_TWAL76eh8&sig=UoUEc2xjUGxLP0awbJv64HXJG14&hl=ro&sa=X&ved=0ahUKEwjCsci5h4_QAhUJaRQKHcR6CkoQ6AEIXTAH#v=onepage&q=numerical%20methods%20that%20work%20forman%20acton&f=false (pg 6-9)
Other variants of this formula:
http://files.ele-math.com/articles/jmi-09-73.pdfA more advanced look at this approach:
https://www.math.ust.hk/~machiang/education/enhancement/arithmetic_geometric.pdf4. My formula
ARCTAN v = 2n x ((2- {2+ [2+ (2+ 2{1/(1+ v2)}1/2)1/2]...1/2}))1/2 (n+1 parentheses to be evaluated)And there is more.
SIN
X = 116.712/188.962 = 0.617648
X = 38.144 degrees, exactly the radius of the three circles used to make the initial calculations for the pyramid
Now, try and solve for X, using only basic arithmetic as a guide.
The controversy created by the measurements of the base of the Giza Pyramid made by C. Piazzi Smyth and W.F. Petrie was solved by D. Davidson who discovered the 286.1 displacement factor of the four sides of the base of the pyramid:
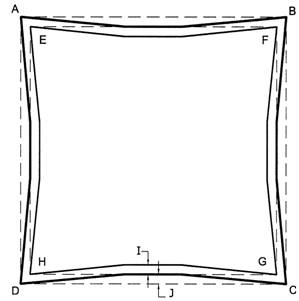
I = 35.8 Pyramid Inches
J = 35.8 Pyramid Inches
286.1/8 = 35.7625
http://thegreatpyramidofgiza.ca/content/#relationship-of-inner-square-circuit-and-outer-square-circuithttp://www.gizapyramid.com/beford%20article%202.htmhttp://the-ultimate-frontier.org/history/Pyramid.htm5.23 + 136.1 + 7.28 = 148.61
5.23 = masonry base = width of the queen's chamber
136.1 = 53.47 x 2.5454
7.28 = 286.1 pyramid inches
[148.61
2 + (233.424/2)
2]
1/2 = 188.962
SIN
X = 116.712/188.962 = 0.617648
The architects of the Gizeh Pyramid must have had at their disposal the arcsin power series, in order to attain at least three significant digits accuracy.

Not even Bhaskara's formula (or Ptolemy's less accurate table of chords with interpolation approximations) will provide the accuracy needed for the final result (moreover, the second formula involves the radian measure and a very precise approximation of π, using at least 355/113).


Substituting the value of 0.617648 on the left side of the equations and solving for x, will lead to an inaccurate result.
In the official chronology of history, ancient Egyptians could barely work out very simple fractions; the 355/113 approximation to π, not to mention raising a number to the 17th power was way beyond their computational capabilities.
Now, let us put everything together.
51.8554/14.134725 = 11/3
1400/11 = 127.27272727
127.272727 = 63.63636363 x 2
51.8554 x 27 = 1400
51.8554 x 1.618034 = 83.904
1.618034 = PHI
83.904 x 0.6366 = 53.413
53.413 x 0.2548 = 13.61
0.02544 = one sacred inch (0.636/25)
136.1 = height of Gizeh Pyramid without the masonry base
Relationship between the two angles:
The other angle of the triangle, 38.145 degrees, is also closely related to the sacred cubit:
38.13 = 60 sacred cubits
And 51.85/38.1 = 1.361 - therefore, all these measurements/dimensions must have been known well ahead of time to the arhitects of the Gizeh Pyramid; but in order to have the actual angle values, they needed to calculate the arctangent of two sacred cubits.
Now, explain to your readers how the ancient Egyptians knew, ahead of time, that 51.85/38.1 = 1.361, where 51.85 and 38.1 are the values of the two main angles and 136.1 is the height of the pyramid without the masonry base.
How did they solve for the values of 51.85 and 38.1 degrees?