Hi QED, do you know of any source to a working numerical Three Body Problem solution of the Sun-Earth-Moon system or a heliocentric system?
As far as I know, none of the solutions or methods can make a heliocentric system.
Poliastro, an astrodynamics software developer shared several numerical Restricted Three Body Problem solutions as applied to the Sun-Earth-Moon system.
Look at this beautiful plot of several numerical methods for the restricted three body problem taken from Harier et al. "Solving Ordinary Differential Equations I". The use of high order Runge-Kutta methods is pervasive in Celestial Mechanics. Happy Monday!
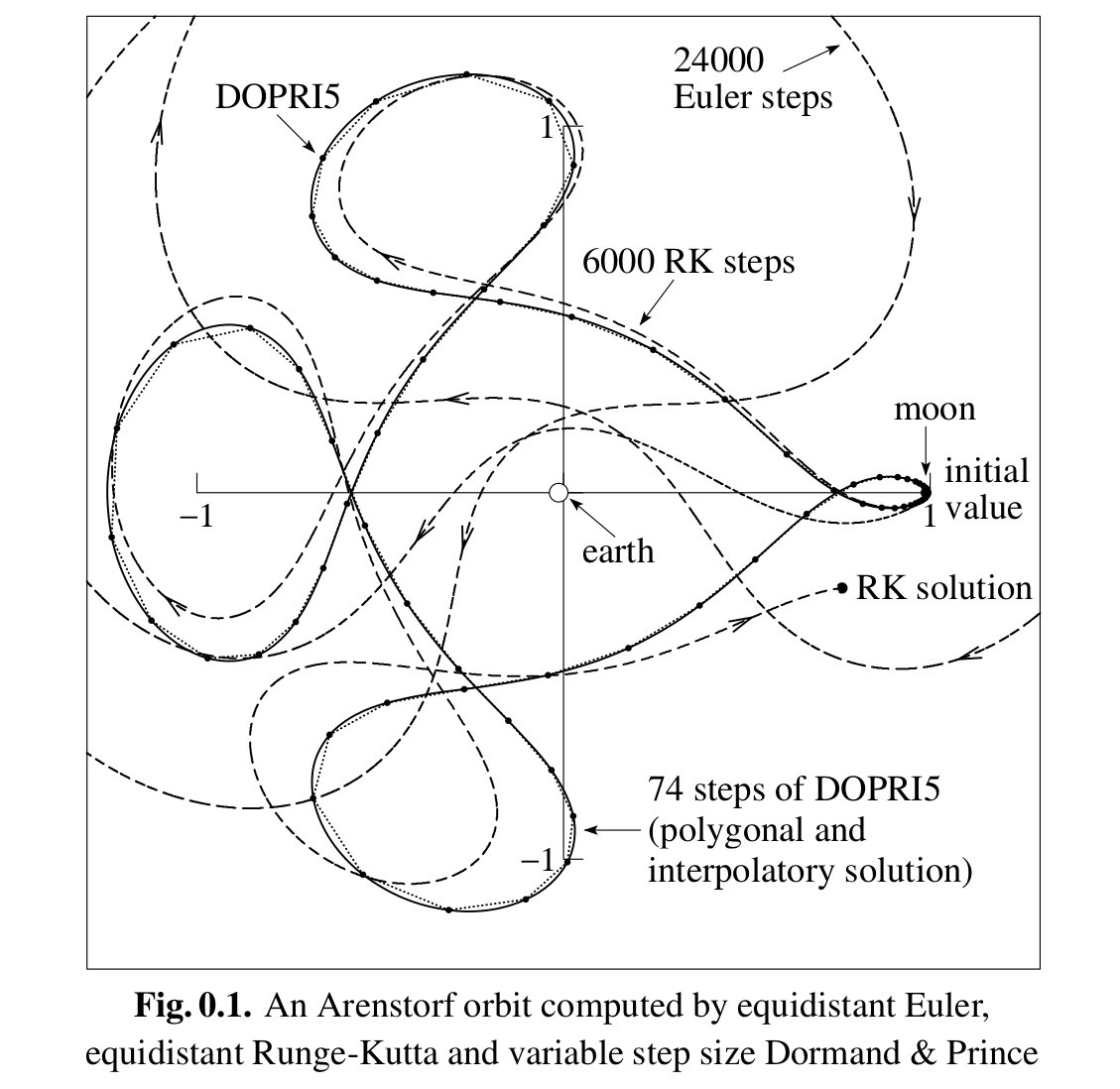
It doesn't quite look like anything like the proposed heliocentric model which claims that it is possible to have a sun with a planet that has a moon.
Also, the solutions must have at least two bodies of the same mass and are incredibly sensitive that fall apart with the slightest adjustment to any parameters or influence by outside gravitational influences
Take a look at the Three Body Problem family gallery:
http://three-body.ipb.ac.rs/Here is an N-Body Orbit Gallery, which showcases the limited orbits that can be made, and which must assume that bodies are of equal mass or mass-less:
http://rectangleworld.com/demos/nBody/The ones that look like a heliocentric system don't exist. I am unable to find that family anywhere in the list of families.
Here are some selected quoted from a New Scientist article:
"Infamous three-body problem has over a thousand new solutions"The new solutions were found when researchers at Shanghai Jiaotong University in China tested 16 million different orbits using a supercomputer.
...
Perhaps the most important application of the three-body problem is in astronomy, for helping researchers figure out how three stars, a star with a planet that has a moon, or any other set of three celestial objects can maintain a stable orbit.
But these new orbits rely on conditions that are somewhere between unlikely and impossible for a real system to satisfy. In all of them, for example, two of the three bodies have exactly the same mass and they all remain in the same plane.
Knot-like paths
In addition, the researchers did not test the orbits’ stability. It’s possible that the tiniest disturbance in space or rounding error in the equations could rip the objects away from one another.
“These orbits have nothing to do with astronomy, but you’re solving these equations and you’re getting something beautiful,” says Vanderbei.
...
Aside from giving us a thousand pretty pictures of knot-like orbital paths, the new three-body solutions also mark a starting point for finding even more possible orbits, and eventually figuring out the whole range of winding paths that three objects can follow around one another.
...
“This is kind of the zeroth step. Then the question becomes, how is the space of all possible positions and velocities filled up by solutions?” says Richard Montgomery at the University of California, Santa Cruz. “These simple orbits are kind of like a skeleton to build the whole system up from.”
To me it appears to be saying that the stable orbits that can be found have nothing that looks like heliocentric astronomy. The system, at its very basic level, is unable to be created.
The "thousands of stable solutions" are scenarios where the bodies have the same mass or where one of the bodies is mass-less. All of these scenarios are incredibly sensitive, and none represent anything that looks like a heliocentric system. They are crazy loopy orbits, based on situations that would not happen in nature, and which fall apart with the slightest touch.
They further appear to admit that they are on the
zeroth step.