There's another chapter in
Earth not a Globe, where great R. tackles the reputation of surveyors and the Geodetic Society.
Main point is - according great R. - if Earth is not a perfect sphere but an oblate ellipsoid, the distance on a meridian measured for the same
difference in latitude must diminish towards the pole.
Or: if you measure the distance of two points on a meridian on the surface of Earth, that show the same difference in latitude, according great R., this distance should be smaller near the pole.
How strange it appears, that one of the most ingenious mathematicians the world ever produced, assumed for certain purposes that the earth was a globe, that it revolved, that its revolutions caused the fluid and plastic matter of its substance to determine towards the equator--causing it to "bulge out" to a greater extent than the diameter in the direction of the axis, and therefore the circumference .at the equator must be greater than the circumference at right angles, or in the direction of latitude; or, in other words, that the degrees of latitude must diminish towards the poles, and yet "men of the greatest skill," with "instruments of the most perfect construction," having availed themselves of "all that science can do," have succeeded in making measurements the most exact "ever made on the face of the earth," have found results the very reverse of all that the Newtonian theory deemed essential to its consistency and perfection! Instead of the degrees diminishing towards the pole they were found to increase; as if the earth were egg-shaped or prolonged through its axis, and not, like an orange, flattened at the sides--"as if;" to use more scientific language, "the earth were an oblong instead of an oblate spheroid."
If I read
Encyclopedia Britannica the result is quite the opposite:
It is possible to determine whether or not Earth is an oblate spheroid by measuring the length of an arc corresponding to a geodetic latitude difference at two places along the meridian (the ellipse passing through the poles) at different latitudes, which means at different distances from the Equator. This can be seen from the figure, in which the geodetic latitude at any point (P) is represented by the angle made between a line perpendicular to the ellipsoidal surface at the point P and the equatorial plane. This angle differs from the geocentric latitude that is determined by a line directed from the point P toward Earth’s centre. Such measurements of arc were made by the astronomer Gian Domenico Cassini and his son Jacques Cassini in France by continuing the arc of Picard north to Dunkirk and south to the boundary of Spain. Surprisingly, the result of that experiment (published in 1720) showed the length of a meridian degree north of Paris to be 111,017 metres, or 265 metres shorter than one south of Paris (111,282 metres). This suggested that Earth is a prolate spheroid, not flattened at the poles but elongated, with the equatorial axis shorter than the polar axis. This was completely at odds with Newton’s conclusions.
In order to settle the controversy caused by Newton’s theoretical derivations and the measurements of Cassini, the French Academy of Sciences sent two expeditions, one to Peru led by Pierre Bouguer and Charles-Marie de La Condamine to measure the length of a meridian degree in 1735 and another to Lapland in 1736 under Pierre-Louis Moreau de Maupertuis to make similar measurements. Both parties determined the length of the arcs by using the method of triangulation. Only one baseline, 14.3 kilometres long, was measured in Lapland, and two baselines, 12.2 and 10.3 kilometres long, were used in Peru. Astronomical observations for latitude determinations from which the size of the angles was computed were made by using the zenith sectors having radii up to four metres. The expedition to Lapland returned in 1737, and Maupertuis reported that the length of one degree of the meridian in Lapland was 57,437.9 toises. (The toise was an old unit of length equal to 1.949 metres.) This result, when compared with the corresponding value of 57,060 toises near Paris, proved that Earth was flattened at the poles. Later, large errors were found in the measurements, but they were in the “right direction.”
The distance measured in Lapland, way north of France, had been measured to be larger than the distance near Paris. But here it
"proved that Earth was flattened at the poles"Also
Wikipedia lists the opposite result:
... The issue could be settled by measuring, for a number of points on earth, the relationship between their distance (in north-south direction) and the angles between their zeniths. On an oblate Earth, the meridional distance corresponding to one degree of latitude will grow toward the poles, as can be demonstrated mathematically.
If you like to examine the Math. for it, you could follow the link in the quote.
A more practical approach to this, using (comparable) less complicated geometry, I put in two slides.
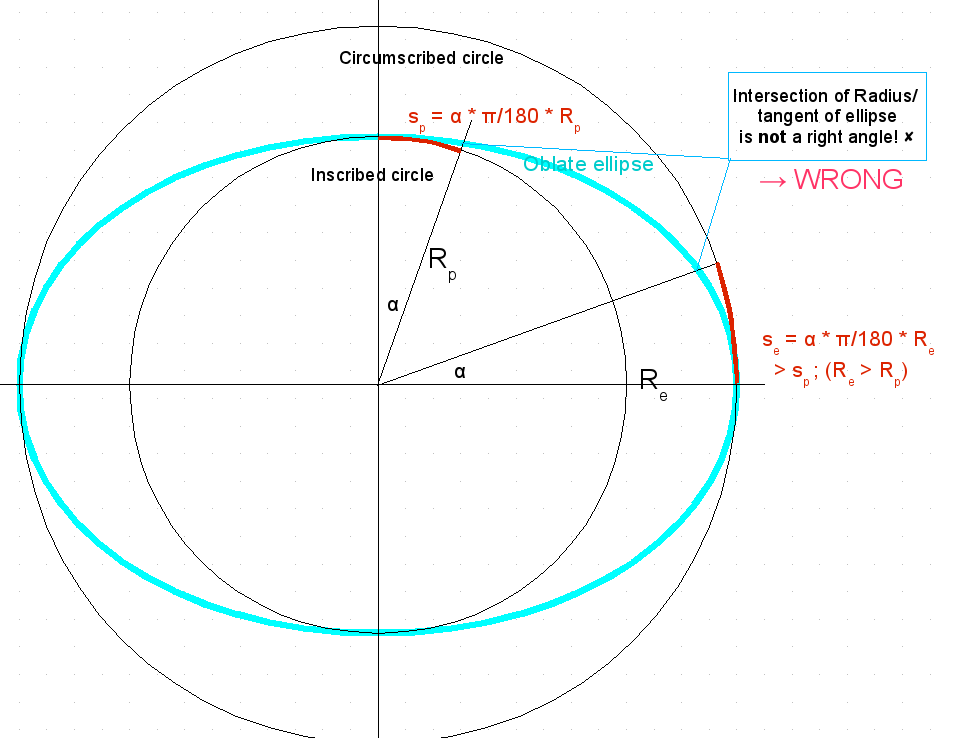
The issue is, which also was my initial false approach, that distances scale with the distance to Earth center - wrong!
What is the sticking point is the [math] curvature of the ellipse. This implies that - as the Earth is flatter near the Pole as near the Equator - you have to go a larger distance near the Pole until you gain the same change for the latitude angle as near the Equator.
This was my initial approach - maybe similar to great R.
This is the more correct approach/approximation based on [math] curvature of ellipse.
I renamed Radii here to "C", to emphasize that these are
Curvature radii.
You can also see, that the approximation of the segments is much better.
