The "three-body problem teaches us a sobering lesson"... "Many physicists may be tempted to see in Newton’s equations of motion and his universal gravitation a sufficient explanation"... An admission that it can't really explain the situation.
Absolutely not. It's the same mistake you make over and over, but I admire your perseverance. That's the "perfect solution fallacy": because there are limitations and difficulties, you seem to assume it doesn't work at all. It would be like saying that because we'll never know the exact numerical value of pi, we really don't have any idea of its value and it could as well be 2 or 5. Just because we don't know everything doesn't mean we don't know anything.
The author doesn't say it comes close either. He gave up on it and says that physicists may be tempted to see that Newton's laws provide a sufficient explanation, but that is not the case. He says that Newton's laws do not provide a sufficient explanation.
You are only speculating that the attempts come close, claiming that "he got close enough" or whatever, when this is not what is said at all.
No serious physicist ever said N-body simulators can't be made, because they do exist and they do work very well.
They say that the N-body orbits require symmetrical systems. Here is physicist David Gozzard:
“ Three hundred and fifty years ago Isaac Newton formulated his theory of gravity Newton's theory unified the heavens and the earth under the same physical laws and neatly explained the orbits of the planets, the motion of comets, and how the moon causes the tides. Although Einstein's general relativity has supplanted Newton's theory as a better model of gravity, Newtonian mechanics got us to the moon and are still used to calculate the trajectories of spacecraft throughout the solar system. In spite of this success and more than three centuries of progress we still do not have a neat set of equations that allow us to calculate the orbital parameters of more than two objects at once. This is called the three-body problem, or more generally the n-body problem. ”
"this is a problem because there are certainly more than two bodies in the solar system. We can get around this by formulating equations that give an approximate solution for motions of three or more objects and since the mid twentieth century we've been able to use computers to simulate the orbits using brute force step by step calculations"
So no, they admit that it's not possible and that they need to use approximations and 'brute force' the orbits.
Author goes on to discuss the discovered orbits:

"any slight perturbation to one of the objects will result in chaos with the body either crashing into its orbital partners or being ejected from the group entirely"
And when going over further discovered symmetrical orbits:
"While physically possible, each of these orbits is more unlikely to exist than the last"
That's the state of Newtonian astronomy.
There are some special things they can do to make it look like a Moon going around a planet around a sun, but those don't work out either. They use the Restricted Three Body Problem, where one of the bodies is of zero mass. Even then, the 'Moon' is still chaotic. The benefit of the Restricted Three Body Problem and the Mass-less moon meant that that the moon would be no longer ejected from the system, as it would usually be. It is confined to what is known as "Hill's Region".
From Scholarpedia:
http://www.scholarpedia.org/article/Three_body_problem by Dr. Alain Chenciner
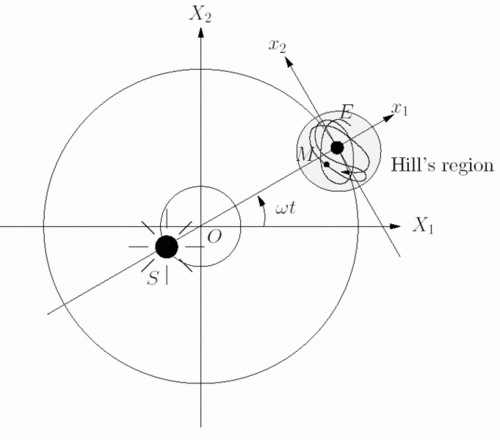
The above depicts a crazy and chaotic moon which even makes a u-turn in mid orbit.
From the text that accompanies the image:
“ The simplest case: It occurs when, the Jacobi constant being negative and big enough, the zero mass body (we shall still call it the Moon) moves in a component of the Hill region which is a disc around one of the massive bodies (the Earth). This fact already implies Hill's rigorous stability result: for all times such a Moon would not be able to escape from this disc. Nevertheless this does not prevent collisions with the Earth. ”
"Zero mass body" -- One of the bodies in the restricted three body problem is of zero mass.
"Nevertheless this does not prevent collisions with the earth" -- It's still chaotic, even in that simplified version.
Even in this weird version with a mass-less Moon, it doesn't really work.
From
Computing the long term evolution of the solar system with geometric numerical integrators by Shaula Fiorelli Vilmart and Gilles Vilmart we see a three body simulation of the Sun-Earth-Moon system created by mathematicians which does use the actual supposed masses of the Earth, Moon and Sun.
Abstract: “ Simulating the dynamics of the Sun–Earth–Moon system with a standard algorithm yields a dramatically wrong solution, predicting that the Moon is ejected from its orbit. In contrast, a well chosen algorithm with the same initial data yields the correct behavior. We explain the main ideas of how the evolution of the solar system can be computed over long times by taking advantage of so-called geometric numerical methods. Short sample codes are provided for the Sun–Earth–Moon system. ”
Sure enough, with the standard algorithm, it fell apart:
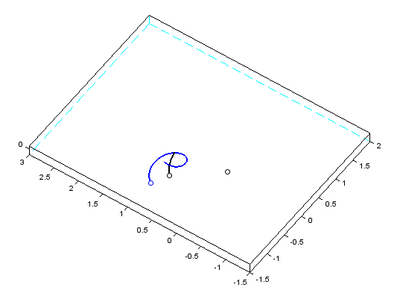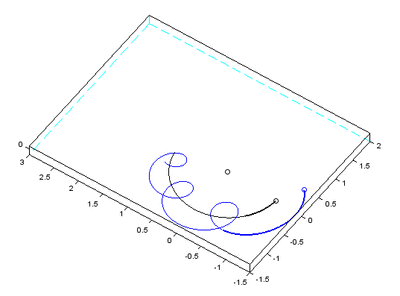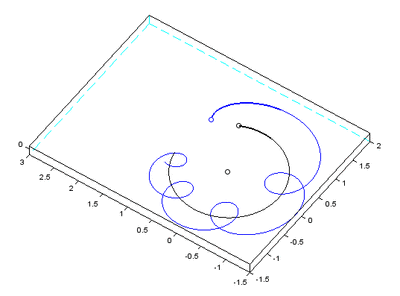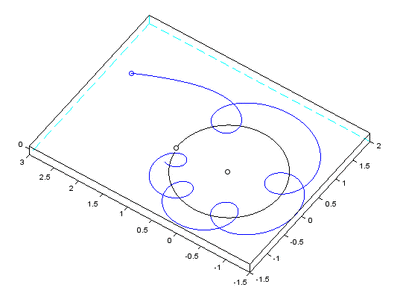
The paper explains that sympectic integrators are necessary and shows a simulation with a working Moon along side this one.
Symplectic integrators are used in particle physics as well (which also has trouble with stability). This
abstract of a particle physics paper says:
“ It has been long understood that long time single particle tracking requires symplectic integrators to keep the simulations stable ”
So again, we see that cheats are necessary.