Yep. Those are the orbits Newton's gravity produces. And here are over a thousand more solutions, as described by New Scientist. Read carefully:
Infamous three-body problem has over a thousand new solutions - New Scientist
For more than 300 years, mathematicians have puzzled over the three-body problem – the question of how three objects orbit one another according to Newton’s laws. Now, there are 1223 new solutions to the conundrum, more than doubling the current number of possibilities.
No single equation can predict how three bodies will move in relation to one another and whether their orbits will repeat or devolve into chaos. Mathematicians must test each specific scenario to see if the objects will stay bound in orbit or be flung away.
The new solutions were found when researchers at Shanghai Jiaotong University in China tested 16 million different orbits using a supercomputer.
All the fresh orbits found are periodic. This means that each object, whether it’s a planet or a proton, ends up where it first began its orbit, with their paths forming three intertwined, closed loops.
“It is impressive that they’ve made the list a lot longer,” says Robert Vanderbei at Princeton University in New Jersey – though he adds that there is “basically an unlimited number of orbits”, so it may be overkill if anyone sought to find them all.
Perhaps the most important application of the three-body problem is in astronomy, for helping researchers figure out how three stars, a star with a planet that has a moon, or any other set of three celestial objects can maintain a stable orbit.
But these new orbits rely on conditions that are somewhere between unlikely and impossible for a real system to satisfy. In all of them, for example, two of the three bodies have exactly the same mass and they all remain in the same plane.
Knot-like paths
In addition, the researchers did not test the orbits’ stability. It’s possible that the tiniest disturbance in space or rounding error in the equations could rip the objects away from one another.
“These orbits have nothing to do with astronomy, but you’re solving these equations and you’re getting something beautiful,” says Vanderbei.
Aside from giving us a thousand pretty pictures of knot-like orbital paths, the new three-body solutions also mark a starting point for finding even more possible orbits, and eventually figuring out the whole range of winding paths that three objects can follow around one another.
“This is kind of the zeroth step. Then the question becomes, how is the space of all possible positions and velocities filled up by solutions?” says Richard Montgomery at the University of California, Santa Cruz. “These simple orbits are kind of like a skeleton to build the whole system up from.”
As suggested by the above article, the field of Celestial Mechanics is still on step zero—the stone age. The found orbits are nothing like heliocentric astronomy and there will be an attempt to use them as a skeleton to "build the whole system up from."
From the linked source paper at the bottom of the article:

All highly symmetric orbits, as Dr. Carroll described.
Symmetrical orbits with two of three masses being identical which "have nothing to do with astronomy" and which "are somewhere between unlikely and impossible for a real system to satisfy."
The phys.org article Scientists discover more than 600 new periodic orbits of the famous three-body problem describes the discovery of other orbits:
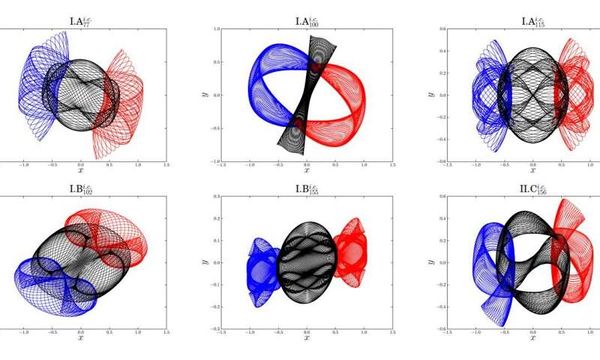
"These 695 periodic orbits include the well-known figure-eight family found by Moore in 1993, the 11 families found by Suvakov and Dmitrasinovic in 2013, and more than 600 new families reported for the first time."
Again, highly symmetrical orbits.
I’d like to draw attention to a few things. First the article:
“This is kind of the zeroth step. Then the question becomes, how is the space of all possible positions and velocities filled up by solutions?” says Richard Montgomery at the University of California, Santa Cruz. “These simple orbits are kind of like a skeleton to build the whole system up from.”
The second is your comment on the above:
“As suggested by the above article, the field of Celestial Mechanics is still on step zero—the stone age. The found orbits are nothing like heliocentric astronomy and there will be an attempt to use them as a skeleton to "build the whole system up from."
The zeroth step is in reference to finding ALL analytical solutions, not the entire field of celestial mechanics, as you inferred.
This zeroth step apparently is being used to build up an understanding of all analytical solutions, not the relatively simple orbits of our solar system.
As I mentioned before, and provided evidence in support, those simple orbits have already been modeled both computationally and analytically - see my two posts on 3 body evidence.
In my opinion, there can be a danger in conflating the two efforts of computational and analytical methods, or generalizing the 3 body problem to celestial mechanics as a whole.