Again, everyone is failing to understand a fundamental concept of visual geometry.
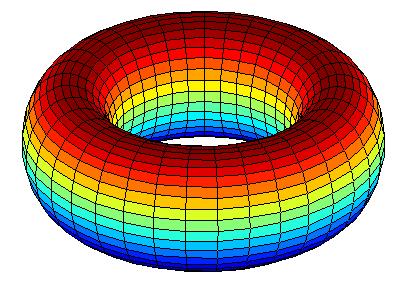
Think about a gigantic torus like the one below, 300m in radius.
Now close the top with a gigantic circular board, just to cover and ignore the central inner circles orange and below.
Go to the center top of such board, go up 20 meters, so you can see better around.
Now look all around you, 360°.
Do you think you would see the external orange or yellow bands?
Of course not, they will be below the "red horizon" bands all around you.
Keep climbing so your head would be few meters over the top most red band. What you see? Only red horizon.
Even that a strong curvature exists from red to external orange, yellow, green, cyan, blue, etc, you can't see that curvature, anywhere you look around you, you only see a red horizon.
You can not see any curvature on the red concentric circles, because there are no vertical curvature there, only flat horizontal circles. The trick here is that all curvature lines start from your point of view in a line that goes away from you.
See, the visual red horizon band is not higher in the center with the sides (left and right) going down, no way, it can't, because when you turn your head, all the red horizon will make a flat plain horizontal line, even that the next red band would be below the horizon, making a curvature from you to ahead, in all directions.
This effect will always happens while you have the object all around you, no matter the altitude you are from that object. It means, if you turn your head all around and still see the object in all directions. The only way to see the curvature from red to orange, yellow, etc, is to get out of the top center of the object, away enough to see the object as a whole in just one direction at certain angle, so you would see the torus as in the image, curvature and all.
Replace the torus with the planet Earth, to see it whole in a single view, curvature and all, you would need to be probably more than 20 to 30 thousand miles in space. While you are close to the planet, no matter the altitude, if you turn your head and still see the planet all around you, the horizon will be a flat horizontal circle line all around you, impossible not to be like that.
And no, you can calculate as much as you want, the only way to see the small degree of curvature as someone calculated in a previous post, is if you slice the planet in vertical half, like a half orange, then go away back and face the cut.
Think with me, if you see ANY horizontal drop at your left of right horizon with the center a little bit up, as in a curvature, what happen when you turn your head to the right? that drop would be more pronounced?, what about on your back? that drop would be adding to be way below you? No, the horizon is a straight flat circle all around you. The next concentric circle further from the horizon would be below the horizon and you can't see it, the horizon image blocks such view. You can, of course, the the inner concentric circle before the horizon, and you will see it all around you, as another flat horizontal circle.
There is not curvature drop to measure while you are sitting on such sphere, the horizon is a flat horizontal circle all around you. In open ocean, the horizon would be at the same distance from you, no matter the direction you look, this makes the horizon a circle around you, leveled, horizontal, no curvature.