Today I found this absolute masterpiece of misuse on the wiki, trying to "prove" that an infinite plane could have finite gravity:
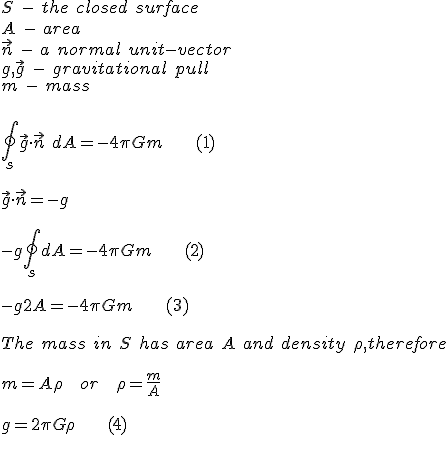
Let's start with statement (1). It appears to be invoking Gauss's law, but there are a lot of problems with it:
- S is a surface, you can't do a single integral over it
- Surface integrals are over dS, not dA
- You don't want flux, you want a triple vector integral
Just these problems are enough to reject this proof.
I’m afraid you are mistaken, it is possible to have finite gravity from infinite plane. The FES has depicted an accurate calculation.
Yes, I am surprised as well.
Your issues:
1. Surface integrals are often done this way in physics.
/integral{2*pi*r*dr}=pi*r^2.
I just computed the area of a circle with a single integral.
2. dS or dA are used interchangeably to denote a surface integral, depending on the textbook.
3. No. A triple vector integral makes no sense here. You want to compute a the flux of gravitational field lines through the closed surface, exactly how you would for an electric field.
The computation is correct and this is not a surprise. You can also have a finite electric field from an infinite plane of charge.
Many, many things on the wiki are incorrect physics or baseless unphysical claims, but this is not one of them.