The earth isn't moving upwards at a set velocity. It is accelerating. More specifically, the surface of the Earth is accelerating upwards into the things above it.
If you walk off of the edge of a chair and go into freefall it will hurt a lot less than if you walk off the edge of a skyscraper. In the skyscraper situation you are inert in space and the Earth has more time to build up velocity and smash into you.
Therefore, in a situation where the Earth is accelerating upwards if you have a broadcasting photon clock light source at the altitude of a chair and a photon clock at the altitude of a skyscraper, from the perspective of a detector on the floor, those photons would be perceived to be hitting it at different rates of reception. The time for the light source on the skyscraper will appear faster than the light source on the chair.
It is also what would happen between the floor and ceiling inside of a rocket ship accelerating upwards through space.
From p.8 of Cosmological Physics by John A. Peacock, PhD. we read the following:
“ Many of the important features of general relativity can be obtained via rather simple arguments that use the equivalence principle. The most famous of these is the thought experiment that leads to gravitational time dilation, illustrated in figure 1.1. Consider an accelerating frame. which is conventionally a rocket of height h, with a clock mounted on the roof that regularly disgorges photons towards the floor. If the rocket accelerates upwards at g, the floor acquires a speed v = gh / c in the time taken for a photon to travel from roof to floor. There will thus be a blueshift in the frequency of received photons, given by Δv / v = gh / c^2, and it is easy to see that the rate of reception of photons will increase by the same factor.
Now, since the rocket can be kept accelerating for as long as we like, and since photons cannot be stockpiled anywhere, the conclusion of an observer on the floor of the rocket is that in a real sense the clock on the roof is running fast. When the rocket stops accelerating, the clock on the roof will have gained a time Δt by comparison with an identical clock kept on the floor. Finally, the equivalence principle can be brought in to conclude that gravity must cause the same effect. Noting that ΔΦ = gh is the difference in potential between roof and floor, it is simple to generalize this to Δt / t = ΔΦ / c^2 ”
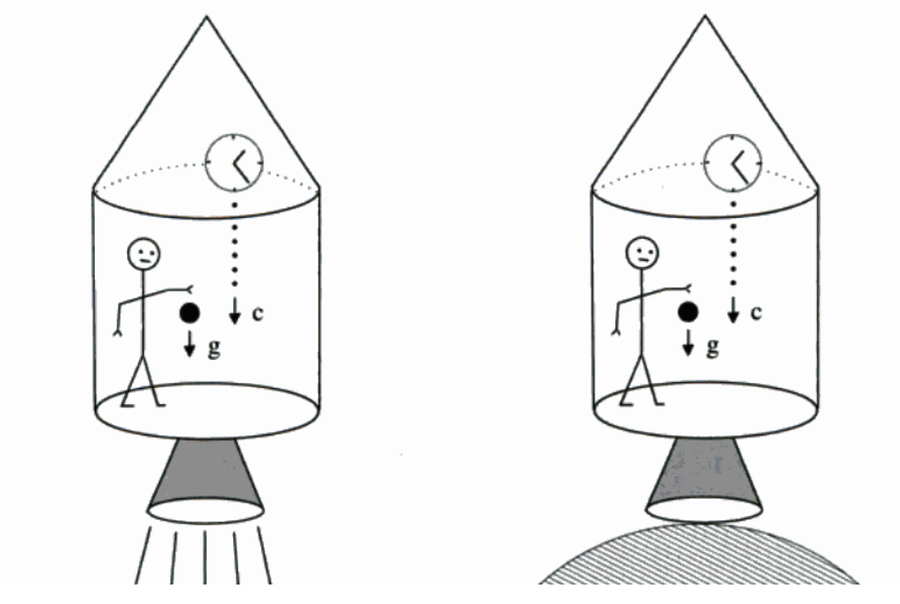
“ Figure 1.1. Imagine you are in a box in free space far from any source of gravitation. If the box is made to accelerate ‘upwards’ and has a clock that emits a photon every second mounted on its roof, it is easy to see that you will receive photons more rapidly once the box accelerates (imagine yourself running into the line of oncoming photons). Now, according to the equivalence principle, the situation is exactly equivalent to the second picture in which the box sits at rest on the surface of the Earth. Since there is nowhere for the excess photons to accumulate, the conclusion has to be that clocks above us in a gravitational field run fast. ”
See the bolded. If you imagine yourself running into the line of photons it is apparent that the clock above you would run fast, because you are running into them. This is a physical explanation for how this works under the concept of upwards acceleration.
In contrast, the Round Earth Theory adopts a non-physical explanation for this which occurs in a hidden layer of reality, in which space is bending to cause the apparent speedup of time at different altitudes. In my opinion this is completely ad-hoc. Physics behaves as if the surface of the Earth is accelerating upwards, but that can't work in RE, so they created this space-bending explanation in an untestable layer of reality which seeks to emulate the physics of upwards acceleration.
In one situation, with upwards acceleration, we can describe what is happening on a physical level for why the rate of reception speeds up when the photons are coming from higher altitudes. In the case of space bending, we cannot. We just call it "space bending" like a magic wand and say that it's physically equivalent to upwards acceleration to explain the otherwise unexplainable. Clearly, there is a difference between the two views.
Why should this space bending mechanism cause photons to travel faster from higher altitudes rather than slower from higher altitudes or no difference at all? What physical reason is there other than to claim that it must be the case because that is what is experienced? One quickly finds a lack of answers.
First, kudos for a good citation. However, I think the argument must be mistaken, because while the bottom of the rocket has accelerated upwards, so has the clock -- meaning, the photons would arrive sooner than expected, but not with a blue shift. Can you find another citation with a similar argument? (I can't.)
IMHO, in this case there would be no time dilation because the top of the rocket gets exactly the same acceleration as the bottom. If there are two clocks, the only time dilation they'd see would be from the trips between them. (That is, if both started at the bottom of the rocket and one went up and down, we'd see dilation from that trip. If both started at the bottom and one went up first and the other later, there would be no dilation. And this would be true regardless of what the rocket does.)
So, if this is indeed a case of a bad lesson in print, then there would be no time dilation for a clock atop a mountain on an accelerating Earth.
If it is a good lesson, then your point stands and I must misunderstand relativity. (I think we can take it for granted that I misunderstand GR. But I think I have this bit right.)
Edit to add: Note that the wikipedia article (
https://en.wikipedia.org/wiki/Gravitational_time_dilation) says "Consider a family of observers along a straight 'vertical' line, each of whom experiences a distinct constant g-force directed along this line ..." and leads to a similar formula. Note carefully the word "distinct," meaning "different". In the textbook's example, the same g-force is exerted on the top and bottom.