A physics illiterate does not tell me where to respond, certainly not in the CN section.
Let us take a look at the full panoply of the physics illiteracy exemplified by rabinoz.
Kelly is completely wrong there because when viewed from an inertial reference frame outside the loop the two opposing lights beams do not travel the same distance and there is no conflict with SR.Only a physics illiterate would make such a statement.
Dr. A.G. Kelly:
 Sure, "the effect could be induced without rotation or acceleration", just as Wang showed, but there is still no detection of absolute linear motion
Sure, "the effect could be induced without rotation or acceleration", just as Wang showed, but there is still no detection of absolute linear motion
But we never needed Herbert Ives to prove that, though you will note that Herbert Ives had a complete polygonal path.Only a physics illiterate does not understand that Herbert Ives proved that the Sagnac is measured, as an example, on a hexagonal path. That hexagon was made up of straight lines: uniform, linear, translational motion.
The physics illiterate REMOVED the link to Ives' paper so that it could not be accessed.
Here it is:
http://www.conspiracyoflight.com/Ives/Herbert_Ives_Light_Signals_Sent_Around_a_Closed_Path.pdf (famous H. Ives experiment: Light Signals Sent Around a Closed Path)
Dr. Ives:
It is the purpose of this paper first to show that
the Sagnac experiment in its essentials involves no consideration of rotation, and second to investigate the results obtained when transported clocks are used.
In 1942, Dufour and Prunier PROVED once again that the Sagnac effect applies to linear paths:
https://www.theflatearthsociety.org/forum/index.php?topic=30499.msg1978311#msg1978311Remember that the contribution to the delay of an increment of the loop is the "vector dot product", v⋅Δl.
So the only motion on a rigid loop like that that can cause a Sagnac delay is the component of the velocity along the length at each point.
Hence rotational motion contributes directly, but any motion normal to loop contributes nothing. Question: why is this physics illiterate allowed to post in the upper forums? Certainly his messages belong to the CN.
Professor R. Wang:
Thus, for a fiber segment having an actual length of Δl, its effective length is Δl cosθ, which is a projection of the fiber onto the motion direction. As shown in Fig. 2, our experiment demonstrates that the effective length contributes the phase difference, not the actual length; therefore, the phase difference ΔΦ is not 4vΔl=cλ, but 4πvΔl cosθ/cλ = 4
vπΔ
l/cλ, which is the dot product between two vectors.
to the delay of an increment of the loop is the "vector dot product", v⋅Δl.The formula is: 4πvΔl cosθ/cλ, which is the CORRECT SAGNAC FORMULA.
For the other experiments Professor Wang does NOT use a dot product anymore.
In fact, by using a PHASE-CONJUGATE MIRROR, the Sagnac formula is derived for an interferometer without loops or area:
SAGNAC EFFECT WITHOUT AN AREA OR A LOOP
https://arxiv.org/ftp/physics/papers/0609/0609202.pdfThe use of a phase-conjugate mirror has permitted new breakthroughs in the experimental science of the Sagnac effect.
The equation which expresses the relationship between interference fringes and time differences is F=dt[c/λ] (where dt = 4Aω/c2).
This experiment shows us two important points. First, it confirms the phase reversal of a PCM and demonstrates the Sagnac effect in an arc segment AB, not a closed path. Second, it gives us important implications: The result, φ = 4πRΩL/cλ, can be re-written as φ = 4πvL/cλ where v is the speed of the moving arc segment AB (where R is the radius of the circular motion, Ω is the rotational rate).
If we increase the radius of the circular motion as shown in Fig. 6, the arc segment AB will approach a linear segment AB, the circular motion will approach the linear motion, the phase-conjugate Sagnac experiment will approach the phase-conjugate first-order experiment as shown in Fig. 4, and the phase shift is always φ = 4πvL/cλ.
The Sagnac effect for a ROTATING LINEAR SEGMENT interferometer IS: 2vL/c2, where v=RΩ.
https://arxiv.org/ftp/physics/papers/0609/0609222.pdfWe have the linear velocity (angular velocity x radius), and the length of the segment: this is the correct Sagnac formula.
The Michelson-Gale formula, by contrast, features NO LINEAR VELOCITY AND NO RADIUS OF THE LOOP, having eliminated the linear velocity from the very start: this is not the Sagnac phase shift formula.
Question: why is this physics illiterate allowed to paper the upper forums with his time-wasting messages?
Not quite. A rigid (non-deformable) loop is not sensitive to linear motion. A demonstration to the contrary for the physics illiterate.
"Sagnac effect is a change in propagation time for light going in a closed path. The time delay Δt appears when a test equipment is rotated with an angular velocity Ώ. Sagnac effect is frequently used in rate gyros in navigational systems. Fiber optics is used with light-speed c inside the fiber in a circular light path. The difference in propagation time Δt for two opposite directions of light is described as
Δt = 4AΩ/c2
Where A is enclosed area. Δt is derived based on an integration of Ω over A.
According to Stokes' rule can an integration of angular velocity Ω over an area A be substituted by an integration of tangential component of translational velocity v along the closed line of length L limiting the given area. This interpretation gives
Δt = 4vL/c2
producing the same value as the earlier expression. This can also be demonstrated by geometrical relations. These two integrations have different physical implications. We must therefore decide which one is correct from a physical aspect. Mathematics can not tell us that. So the decision is whether the effect is caused by a rotating area or by a translating line. Since Sagnac effect is an effect in light that is enclosed inside an optical fiber we can conclude that Sagnac effect is distributed along a line and not over an area. No light and no rotation exists in the enclosed area. Sagnac detected therefore an effect of translation although he had to rotate the equipment to produce the effect inside the fiber.
We conclude that the later expression
Δt = 4vL/c2
is the correct interpretation."
http://www.gsjournal.net/Science-Journals/Research%20Papers-Astrophysics/Download/2159 "Sagnac effect is distributed along a line and not over a surface. The assumption that starts from an integration over a surface (2Aw; rotation) is mathematically correct (due to Stokes' rule) but equal to a line integral (vL; translation). We must decide if the reason is a translating line or a rotating surface from a physical point of view. The rotation theory is correct only mathematically. Since the effect is locked inside an optical fiber the translating line is the correct interpretation. Classification as a rotational effect is wrong."
Therefore, the formula for the Sagnac phase shift which features the area and the angular velocity IS INCORRECT. Only the formula which includes the linear velocity is CORRECT.
I'll ignore your claims where you claim to be smarter that Michelson who knew that he was on a rotating Globe.Michelson used the CORIOLIS FORMULA.
Very easy to prove.
Spinning Earth and its Coriolis effect on the circuital light beamshttp://www.ias.ac.in/article/fulltext/pram/087/05/0071The derivation for the Coriolis effect formula.
Classical Interpretations of Relativistic Phenomena
https://file.scirp.org/pdf/JMP20120200009_86423451.pdf (pg. 198)
The formula for the fringe measurements caused by the Coriolis effect IS THE SAME as the formula derived by A. Michelson for the Sagnac effect as applied to the rotation of the Earth.
The Coriolis effect (not the Sagnac effect) is responsible for the non-null result of the Michelson–Gale experiment assisted by Pearson and the experiment of Bilger et al.
As was shown above, the Sagnac phase shift formula featuring the area and the angular velocity is the incorrect mathematical expression.
That is why the derivation published by A. Michelson is completely wrong: the data for the Michelson-Gale experiment was obtained by measuring the Coriolis effect and not the Sagnac effect.
The physics illiterate is at it again, using an unbelievable deceptive argument:
Note that the expression for the incremental delay caused by a small length, Δl, is Δϕ = 4πv⋅Δl/cλ is a vector expression.
The incremental delay is not simply found from the product |v| . |Δl| but the vector dot product, v⋅Δl.It was shown above that the vector expression means this:
Professor R. Wang:
Thus, for a fiber segment having an actual length of Δl, its effective length is Δl cosθ, which is a projection of the fiber onto the motion direction. As shown in Fig. 2, our experiment demonstrates that the effective length contributes the phase difference, not the actual length; therefore, the phase difference ΔΦ is not 4vΔl=cλ, but 4πvΔl cosθ/cλ = 4
vπΔ
l/cλ, which is the dot product between two vectors.
to the delay of an increment of the loop is the "vector dot product", v⋅Δl.The formula is: 4πvΔl cosθ/cλ, which is the CORRECT SAGNAC FORMULA.
For the other experiments Professor Wang does NOT use a dot product anymore.
The equation which expresses the relationship between interference fringes and time differences is F=dt[c/λ] (where dt = 4Aω/c2).
This experiment shows us two important points. First, it confirms the phase reversal of a PCM and demonstrates the Sagnac effect in an arc segment AB, not a closed path. Second, it gives us important implications: The result, φ = 4πRΩL/cλ, can be re-written as φ = 4πvL/cλ where v is the speed of the moving arc segment AB (where R is the radius of the circular motion, Ω is the rotational rate).
If we increase the radius of the circular motion as shown in Fig. 6, the arc segment AB will approach a linear segment AB, the circular motion will approach the linear motion, the phase-conjugate Sagnac experiment will approach the phase-conjugate first-order experiment as shown in Fig. 4, and the phase shift is always φ = 4πvL/cλ.
The Sagnac effect for a ROTATING LINEAR SEGMENT interferometer IS: 2vL/c2, where v=RΩ.
https://arxiv.org/ftp/physics/papers/0609/0609222.pdfWe have the linear velocity (angular velocity x radius), and the length of the segment: this is the correct Sagnac formula.
This is the formula published by Michelson in 1904 and 1925:
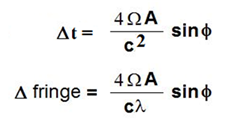
Michelson thought that this expression for the fringe shift measured the Sagnac effect due to Earth's rotation (due to a Sagnac interferometer).
However, this is the CORIOLIS EFFECT FORMULA for circuital light beams.
Here it is:
Δt = 4AΩsinΦ/c^2 (where Φ is the latitude)https://www.ias.ac.in/article/fulltext/pram/087/05/0071https://file.scirp.org/pdf/JMP20120200009_86423451.pdf (page 198)
The vector potential of Coriolis forces in a rotating frame of reference and the effect of these forces on counterpropagating beams of light is a well-established subject in physics.
This formula for the Coriolis effect on circuital light beams can be derived by an undergraduate student of physics.
By contrast, the correct Sagnac effect formula is:
Δt = 4vL/c^2The Michelson-Gale formula, by contrast, features NO LINEAR VELOCITY AND NO RADIUS OF THE LOOP, having eliminated the linear velocity from the very start: this is not the Sagnac phase shift formula.
The Coriolis effect formula derived by Michelson features only the area and the angular velocity. Since vr = r x Ω, and r = 6,378.164 km, the Sagnac is larger in magnitude than the Coriolis effect by at least the r = 6,378.164 km factor.
It is obvious that the fringe shifts recorded by A. Michelson and H. Gale did not register the Sagnac effect at all; only the Coriolis effect (much smaller in magnitude) was observed.
The value of the main term of the Coriolis effect for an interferometer (in the shape of a rectangle, trapezoid, annular sector) located away from the geometric center of the rotation (of the turntable/Earth/circle) will be THE SAME as the value of the Sagnac effect for the same interferometer whose center of rotation now coincides with that of the turntable/Earth/circle.
This is a Sagnac interferometer, whose loop coincides with the center of rotation:

This is a Sagnac interferometer, whose loop IS AWAY FROM the center of rotation, featuring two different radii (from the center to both legs of the interferometer):

Since now one has two different radii to deal with, the Coriolis effect will first be recorded/registered, using this formula:
Δt = 4AΩ/c^2
But this is NOT the true Sagnac effect.
The true Sagnac effect will be:
Δt = 4vL/c^2
v = (RADIUS TO THE LONG LEG OF THE INTERFEROMETER) X angular velocity
L = long leg of the interferometer
This is what Michelson cleverly REMOVED from his equation: the RADIUS OF THE EARTH ITSELF, 6,378.164 KM.
That is, the Sagnac effect will be larger than the Coriolis effect upon the interferometer by a factor of at least 6,378.164 km.
This effect WAS NEVER RECORDED BY MM, MG, H experiments.
This means that the Earth is stationary.
If this type of interferometer is used, being located away from the center of rotation, one is going to measure the following effects:
1. THE CORIOLIS EFFECT (which was recorded by Michelson-Morley, Michelson-Gale and Hammar)
The Coriolis effect will be:
4ΩA/c^2 (this term is multiplied by sinΦ, where Φ is the latitude)
2. THE TRUE SAGNAC EFFECT, which was NOT recorded by MG, MM, H exp.
Then the value of the Sagnac effect will measure: 4ΩrL/c^2, where r is the distance from the center of the circle to the upper leg of the rectangle.
The Coriolis effect is 4ΩA/c^2, where A = Lh.
The Sagnac effect value will be 4ΩrL/c^2.
The ratio will be r/h.
Thus, by contrast, A. Michelson and H. Gale actually calculated the Sagnac formula for a rectangle with sides 2010 ft (612.65 m) and 1113 ft (339.24 m) which is placed at the center of the rotation.
This is equivalent to calculating main term of the Coriolis effect formula, if we place the rectangular interferometer at the surface of the Earth, as was done in the Michelson-Gale experiment.
The ratio of the correct Sagnac formula to the Coriolis effect formula will be:
6,378.164/0.33924.
3. THE ORBITAL SAGNAC EFFECT
Not recorded by the MM, MG and H experiments.
The orbital Sagnac effect is 60 TIMES larger than the rotational Sagnac effect.
4. THE GALACTIC SAGNAC EFFECT
The galactic Sagnac effect is 8 times larger than the orbital Sagnac effect, thus 480 times larger than the rotatational Sagnac.
The fact that the MM, MX and H experiments recorded ONLY the Coriolis effect, means that the Earth is stationary.
IF THE EARTH HAD BEEN ROTATING AROUND THE SUN, OR AROUND ITS OWN AXIS, the Michelson-Gale interferometer (a Sagnac interferometer) SHOULD HAVE RECORDED THE ORBITAL AND ROTATIONAL SAGNAC AT ONCE. In fact it only recorded the Coriolis effect of the ether drift rotation.
For the physics illiterate, FURTHER PROOF that if two radii are present, one is going to measure first the Coriolis effect:
https://link.springer.com/article/10.1023/A:1023972214666https://arxiv.org/pdf/gr-qc/0103091.pdfCoriolis Force and Sagnac Effect
Because of acting of gravity-like Coriolis force the trajectories of co- and anti-rotating photons have different radii in the rotating reference frame, while in the case of the equal radius the effective gravitational potentials for the photons have to be different.


An interferometer with DIFFERENT RADII (located away from the center of rotation) will manifest the Coriolis force in the form of a phase shift 4AΩ/c2.
This formula is the equivalent of a Sagnac phase shift, where the interferometer is placed concentric with the center of the rotation of the turntable.
The real Sagnac phase shift will feature a linear velocity and the radius of the loop.
The physics illiterate has to understand that the Sagnac effect is caused by the POTENTIAL, the Whittaker ether waves:
https://www.theflatearthsociety.org/forum/index.php?topic=30499.msg2039636#msg2039636