There is something that seems wrong with the way the earth rotates around the Sun. Consider the following image that we are taught in school:
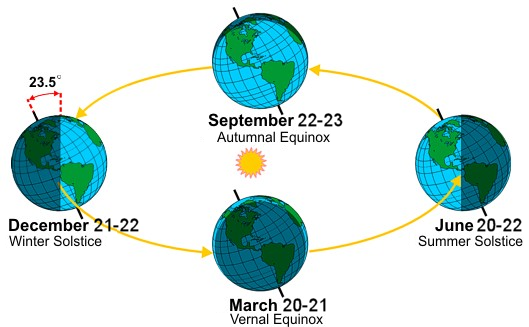
Assume that New York City is in its Solar Noon (look at where New York City is in the top and bottom September and March figures in the above illustration). After 6 months the motions suggests that New York City will be in darkness during its noontime.
I’d like to point out that, like the flat earth animation graphic, that picture you’ve chosen of earth’s orbit about the sun is just a visualization. It’s illustrating a point about tilt and equinox/solstice and isn’t meant to be a scale, accurate representation. The globe earth is a copy and paste icon massively larger and close to a tiny cartoon sun.
But, your question is understandable nonetheless...
Some Rough Calculations
Napkin Calculation 1
Day = 24 hours
Year = 365 days
365 days / 2 = 182.5 days in 6 months
24 hours x 182.5 days = 4380 hours in 6 months
4380 hours / 360 (since the sun rotates around the earth 360 degrees in one day) = 12.16666 hour offset
Earth should be offset by 12.16666 hours (similar to the above image)? NYC should be in night?
Yes. The approach you took is confusing, but the solar day and sidereal day will be offset by about 12 hours, and the side of the world facing the sun at the starting gun will be facing away from the sun at the halfway point.
Napkin Calculation 2
According to RET particulars, the earth doesn't rotate at exactly 24 hours a day, and the earth doesn't have an exactly 365 day year, which is why we have to change times and add a leap year every 4 years.
Sidreal Day = 23.933333 hours
Sidreal Year = 365.25636 days
365.25636 days per year / 2 = 182.62818 days in 6 months
23.933333 hours per day x 182.62818 days = 4370.90104712394 hours in 6 months
4370.90104712394 / 360 (since the sun rotates around the earth 360 degrees in one day) = 12.14139179 hours offset
Earth should be offset by 12.14139179 hours? NYC should be in night?
Again, don’t agree with the method, but same result: an “offset” as should be expected between a star field frame of reference and a solar frame of reference at the half yearly mark.
Napkin Calculation 3
Some sources say that the earth "actually" rotates 360.98 degrees per day.
360.98 degrees in a day x 182.62818 days in 6 months
= 65925.1204164 degrees in 6 months
ans / 360.98 = offset is 183.62818 degrees.
Earth should be offset by 183.62818 degrees? NYC should be in night?
--- --- ---
Corrections with the 360.98 figure
Using 360.98 degrees per day in the second calculation, replacing 360 with 360.98, gives an offset of 12.1082 hours. The offset still says that NYC should be in night.
Replacing 360 with 360.98 in the third calculation gives an offset answer of 182.625 degrees. The offset still says that NYC should be in night.
---
I may be going about this entirely wrong. Can I have some help with this seemingly glaring problem?
Even when cross mixing sidereal and synodic parameters, you’re still getting a affirmation that there’s about a half a day/half a rotation delta between sidereal and solar. And yes, if NYC was at high noon at the start, it’ll be in darkness at half way around the orbit.
The fact that the earth orbits while it rotates is why.
Solar day is 24.000 hours per 360.986 degrees.
Sidereal day is 23.934 hrs per 360.000 degrees.
After halfway thru 365.24 solar days (which is also 366.24 sidereal days) the two measures will be offset by about 12 hours, which means it will be oriented the same as it was to the stars when it started the year but 180 degrees out in relation to the sun.