1121

Flat Earth Investigations / Re: Possible Issue with Solar Noon in Round Earth Theory

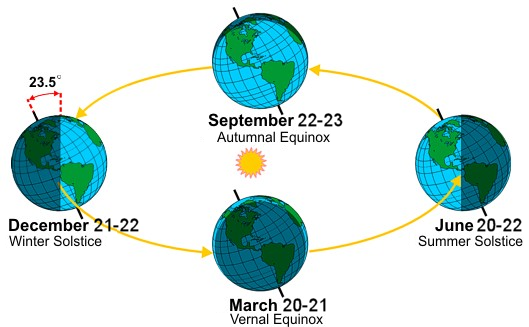
« on: April 26, 2018, 07:21:35 PM »

Consider if the September Equinox in the above illustration was at Solar Noon. Solar Noon is when the Sun is directly overhead.

After 1 Solar Year the Solar Noon can't be Solar Noon plus 5+ Solar Hours. The sun would be pointing off into space. How does that work?

You're right. It can't. That's why the last solar noon (on the 365th day) happens before the end of the solar year. Those two moments don't coincide. If starting the measure of the solar year is at the equinox (you've chosen September instead of March, but whatever), that isn't at solar noon either (necessary; I mean it could be on rare occasions.)

Solar day doesn't have to start at solar noon either. You could pick any measurable moment of sun elevation and use that as a starting point. But the day is the amount of time to rotate and see the sun back at that point.

Similar with solar year. Doesn't have to start count at an equinox. It's just a good marking point. But the amount of time for the earth to complete its orbit to get back to that point, relative to the sun, is a solar year.

For illustration purposes, you can start the measure at solar noon and, for the sake of understanding, assume that is also the time of the vernal (Spring) equinox. Let the motions occur and at the next vernal equinox, it won't be solar noon. That's because that 365th solar noon happened earlier, before the equinox was reached. When the equinox is finally reached (completing the solar year), about 5.5 to 5.8 more hours will have elapsed because the earth kept rotating until vernal equinox.

1122

Flat Earth Investigations / Re: Possible Issue with Solar Noon in Round Earth Theory

« on: April 26, 2018, 07:05:49 PM »

Lets Recap

I have several pages giving a rebuttal is that the Solar Day and Solar Time is unconnected to the Solar Year. There are 24 hours in a Solar Day and 356.24 Solar Days in a Solar Year. Where does the .24 come from? The argument I am hearing is that the two are "unconnected". There are posts with arguments that the two are "arbitrary" and the names Solar Day and Solar Year coincidental. Lets work with that.

I stopped reading here, and I haven't scrolled down to see if anyone else has responded.

Tom,

I can appreciate if you feel kind of like you're being ganged up on, and I don't want to contribute to what might feel like a mob. I think we're all independently trying to explain to you the same thing, though maybe in different ways. And there's obviously history with some of you that is leading others to respond more caustically.

I, for one, don't like to discuss things that way. But I do wish I could help you work through the question, but your recap is not right, and you can't use that as a place from which to start to "work with."

You seem to expect something to be true that isn't.  These solar days, solar years, etc. are not "arbitrary." They aren't "unconnected." They're just not connected in a manner that you consider whole.

1 rotation of the earth with respect to the sun is a solar day. That's not arbitrary. It's 1. 1 day. 1 solar day.

1 orbit around the sun is a solar year. That's not arbitrary. It's 1. 1 year. 1 solar year.

The solar day happens 365 times in 1 solar year, but then there's a fractional period of rotation that must occur before the orbit of 1 solar year is complete. That's not arbitrary. It's measurable. It's "arbitrary" I suppose, but with good reason, that you might want to choose a starting point for measuring the year at an equinox or solstice. In this case, via convention (call it arbitrary) we use the vernal equinox. But the number of earth rotations (relative to the sun) during the length of that orbit to the next vernal equinox is not arbitrary. They happen naturally, are measurable, and the solar day doesn't line up with the solar year in a whole number. The earth reaches a point in its orbit around the sun a little before the vernal equinox when it completes its 365th solar day rotation.

That's where the extra time is coming from. The earth rotates a little more while it has to complete that orbit, returning to the point of the vernal equinox.

Calling things "arbitrary," "coincidental" and "unconnected" indicates you aren't absorbing what's being explained. Some things, like words or units of measurement might be "arbitrary" or based on something that is a matter of convenience or convention, but what we are measuring aren't. And you can't consider what's being measured as "unconnected" just because the way we measure doesn't use units that divide evenly as integers. Fractions are a way of life in the world.

I hope that helps. (If I'm redundant and someone else has already made that point, I apologize, but I hope you aren't being resistant just because you feel defensive or ganged up on.)

1123

Flat Earth Theory / Re: The Horizon is Always at Eye Level

« on: April 26, 2018, 04:49:01 AM »

I confess I don't understand the horizon in a flat model. As I think I understand it, the FE "horizon" is a perceptual one (apparent) that occurs level to height of viewer (0° to the horizontal), but isn't a measurable distance. It depends on acuity (resolution) and obscuring factors in the air.



The horizon on a convex curved surface is a geometric point, calculated by height of viewer and radius of the curve, but it's always some angle below the horizontal, though appearing to be at horizontal for low values of h relative to r.



If so, then I think that if you can demonstrate that the horizon drops below horizontal eye level with increasing height, it supports a curved surface. If the horizon appears consistently at the horizontal at all values of h, it would support the flat earth claim.

Does that make sense?

If so, the next step is to find agreement on how best to measure and document the horizon vs. "eye level" at different heights above the surface. I have some ideas, and I have easy access to viewpoints from sea level to 1500' with clear views to an ocean horizon, though catching a non-hazy day for a good horizon contrast is hit and miss this time of year.

I like the idea of a water level that's not cumbersome to tote on a hike, but I'd want it to be set up on a stable platform or tripod rather than handheld as in that video. Plus the camera would have to be stabilized and aligned with the leveling site.

I think about it, but would appreciate input or feedback, particularly from "horizon always at eye level" proponents.

1124

Flat Earth Investigations / Re: Possible Issue with Solar Noon in Round Earth Theory

« on: April 26, 2018, 03:03:38 AM »

I would note, even this simulation isn't exact. Look at the times of the equionoxes here if you wish. https://www.timeanddate.com/calendar/seasons.html

It’s not exact because that’s not what it’s meant to be. Actual equinox and solstice times vary year to year. This is generic.

It’s a nice aid for demonstrating how solar days and sidereal days are related. But the times are purely representative and not actual or predictive. And unfortunately for explaining to Tom how solar days don’t fit as whole integers into a solar year, or show how the time of vernal equinox varies from year to year, it wasn’t coded for that. It shows a single solar year divided crisply into 365 solar days and 366 sidereal days with the earth returning to the same spot in its orbit around the sun. That’s what Tom thinks should be true of a globe earth/sun model if it were reality. but the solar year, equinox and earth rotations aren’t synchronized that way. The animation is simplified for the introductory student.

1125

Flat Earth Investigations / Re: Possible Issue with Solar Noon in Round Earth Theory

« on: April 26, 2018, 02:52:13 AM »

Look at the second animated image I added above. Solar Time returns to the same position after one year when it returns to the Equinox it started on. The Solar Time is opposite on the opposite Equinox. The Solstices are opposites too.

If there is a difference over the year and the Solar Day is just arbitrarily related to the year, why are there exact opposites?

That’s a teaching tool to demonstrate the relationship between solar and sidereal days. It’s using generic times and isn’t accounting for the extra .24 of a day. Hard to manipulate on mobile, but it resets at the vernal equinox at exactly 356 solar days and 366 sidereal days.

It’s not a calculator for actual equinox and solstice times. It’s for illustrating the concept to students. It ought to help you resolve the question you had had the opening of this topic. But I can understand why it might be confusing in trying to understand the relationship of solar days to solar years. It wasn’t coded for that.

Look at it for what it is intended: a simplified interactive illustration of the solar/sidereal relationship concept.

1126

Flat Earth Theory / Re: The Horizon is Always at Eye Level

« on: April 25, 2018, 10:10:43 PM »

Define "eye-level".

And also, we've discussed this at length before and the flat earthers didn't understand any of the evidence presented.

Wasn't there an experiment performed a short while ago that soundly disproved this, using a u-tube filled with coloured water?

Yowza!  That's pretty much what I was thinking about doing.

But I thought I'd invite the community here to talk it through first: what am I measuring. How should I be sure to do it (and document it). And make predictions about the results or analysis of predicted results. Do all that before putting in the effort.

The wiki is making the claim and using that as the basis for a flat earth argument about horizons. I thought it might be worthwhile to test the claim.

1127

Flat Earth Theory / Re: The Horizon is Always at Eye Level

« on: April 25, 2018, 10:01:31 PM »

Define "eye-level".

I hadn't thought to ask that question, but good idea to define so that we're all on the same sheet of music.

I assumed "eye level" was a sight line at same level as the eye, parallel to the surface.



The same geometry would apply if the surface is curved, but replace the last phrase with "parallel to a tangent of the curved surface."

"The horizon is always at eye level" means (to me) that no matter the height above the surface, the horizon will appear in line of sight with no inclination or declination. It "rises" to eye level without having to angle sight line down from the horizontal.

Is that correct? (Flat earth proponents?) 

1128

Flat Earth Theory / The Horizon is Always at Eye Level

« on: April 25, 2018, 09:03:48 PM »

"A fact of basic perspective is that the line of the horizon is always at eye level with the observer."
https://wiki.tfes.org/Horizon_always_at_Eye_Level

If this "fact of basic perspective" is true, I believe it can only be true for perspective at eye-level over a plane (flat) surface).

For perspectives from an eye-level height of a plane tangent to a curved surface, the horizon will not always be at eye-level.

This would make observations of horizon relative to eye-level a potentially good indicator of whether or not one is viewing that horizon over a flat or a curved surface.

Is there anything wrong with that line of reasoning?

1129

Flat Earth Investigations / Re: Possible Issue with Solar Noon in Round Earth Theory

« on: April 25, 2018, 07:25:30 PM »

In 2016, the March equinox occurred at 04:30 (UTC) on March 20th.

Start the clock. Start the calendar.

The earth keeps rotating and begins its orbital trek around the sun. 365 days after we've started our clock, we approached 04:30 UTC on March 20th, 2017. The earth had rotated 365 times in relation to the sun (366 times in relation to the stars) during that trek. But the earth hasn't reached the same spot in its orbit as it was when we started the clock. It still has a little ways to go.

So the earth keeps spinning and we don't hit the equinox point (plane) until 10:28 UTC on March 20th, 2017. It doesn't change anything as far as our clocks are concerned. It still feels like 10:28 (or whatever time zone you're in). But the time of day of reaching that orbital spot has gotten later by almost 6 hours. We note it, but the earth is still spinning on its axis and we keep the clock rolling and keep ticking off the calendar  as we start a new trip around the sun.

Another year passes and we confront the same situation as before. It's now March 20th, 2018, but the time of equinox is later in the day, again. Now it's 16:15 UTC. Same reason as before. The earth hasn't completed a full orbit in exactly 365 calendar days and still needs to finish the last bit of that orbit. But the earth keeps rotating and a little under 6 hours, we reach the equinox.

That's two trips around the sun and we've seen the equinox slip 11 hrs and 30 minutes. It isn't a set time difference each time. It varies, but it's within a range of 5 1/2 to 6 hours. But still we roll with it, start the trip around the sun again. On March 20th, 2019, the equinox arrives 21:58 UTC. Same reason. Same approximate time slippage.

A fourth trip around the sun produces yet another slippage in the time of equinox. It's now occurring at 03:50 UTC. But what day? If we didn't input a "leap day" sometime prior, the equinox would fall on 03:50 21 March (UTC). But we do, adding a day to February 2020 and catch the calendar up all in one fell swoop. We basically add 24 "extra hours" to make up for the fact that our calendar had slipped 23 hrs and 40 mins over the previous 4 orbits around the sun, using the equinox as a marker.

It's not perfect because we haven't restored the equinox to the exact minute that it was back in 2016, but that variance takes much longer to matter to our calendar date keeping. But those ~6 "extra hours" per year are simply due to the fact that the solar day DOESN'T "fit" into the solar year as a whole integer. The earth's rotation isn't perfectly matched with the earth's orbit about the sun. We complete the 365 solar rotations (or 366 sidereal rotations) just a little short of 1 full orbit about the sun.

And yes, there are other factors that affect the calculus, but those are less impacting on our annual calendars as is the mismatch of solar day with solar year. Precession, wobble, drag...some of those effects take centuries, millenia or eons to matter, phenomenological. They do matter to astronomers who must be precise, but not to our daily calendar life. Those "extra hours" do matter to us regular folks because we'd notice that seasons would appear to gradually shift during the calendar if we didn't make those "leaping" adjustments.

It would be nice and tidy if we didn't have to worry about those adjustments and the time piece of the sun/earth was tuned for our convenience. But it's not, and it doesn't have to be. We get "extra hours" in a solar year because of that and they don't appear out of nowhere.

1130

Flat Earth Investigations / Re: Possible Issue with Solar Noon in Round Earth Theory

« on: April 25, 2018, 06:37:04 PM »

The equinox shifts 6 hours a year?

The equinox's variation occurs with a rotation of about once every 25,772 years. The shift takes a very long time. At the moment The Equinox is aligned with the constellation of Pisces, and we are moving into the "Age of Aquarius." The time between Zodiac points is about 2,150 years.

You are still trying to decipher where the "extra hours" in the solar year come from, right? So you need to talk apples and apples. The variation you're speaking of there has to do with movement of equinox along the plane of earth's orbit, aka the ecliptic. That's oranges. The apples are the yearly shift in time when the equinox occurs from an earth perspective, and that is just under 6 hours each year. As in about 1/4 of a 24 hour day. That's where you're "extra hours" are coming from.

If you've moved on from that new "problem" too and are talking now about something else dealing with the cyclic precession of the earth's rotational axis, I apologize. But it seems to me you're getting yourself wound around the axle, trying to work in all the complex motions of earth's rotation and orbit to understand the simple notion that the earth doesn't rotate a whole number of days during the course of one orbit around the sun. That's all the extra hours are is that those two parameters (solar day and solar year) aren't integrated as a whole number.

Forget the 25K year precession cycle. It has nothing (very little) to do with the so-called "problem" you think you've identified.

The Salon article you linked was pretty good, I thought. Cheeky explanation of what can be a confusing subject, I know. Your first problem (which apparently wasn't resolved to your satisfaction) was why at the exact halfway point of a solar year, NYC isn't oriented toward the sun as you presumed it should be. Your second was the "mystery" of where the "extra hours" came from in a solar year. Both of those questions are addressed in the Salon article pretty well. You may not like that it "doesn't fit" in an orderly way, but the universe doesn't conform to how we wish we could measure and quantify. We choose from nature what we want to use as a standard reference, and if we find that there's variation or deviation from what we thought, we either have to adjust our methods or pick a new standard. We can't expect the universe to conform to what we think would make calculations easier or more aesthetically ordered.

1131

Flat Earth Investigations / Re: Possible Issue with Solar Noon in Round Earth Theory

« on: April 25, 2018, 10:02:01 AM »

The Sun needs to get back to the point of the Equinox under the definition of a Solar Year. It has to match up with the Solar Day.

First sentence, I agree. It “needs to” for the definition to be true.

But what I’m not getting is why you think the second sentence is a “has to” situation and, if it doesn’t, it’s a problem.

It clearly doesn’t meet your “has to” expectation since Equinox occurrence slides later by about 5.8 “extra hours” each year, and would keep sliding forward into the calendar year if we didn’t add a day to the calendar every four years.

I’m not picking up on why this is a problem. Solar days don’t “have to” fit neatly  and non-fractionally into the solar year. Not in reality, and not by definition.

1132

Flat Earth Investigations / Re: Possible Issue with Solar Noon in Round Earth Theory

« on: April 25, 2018, 09:59:18 AM »

Equinox is just the sun passing the equatorial plane, its not a fixed point.

Right. And there’s nothing in that definition requiring it to occur after a whole number of 365 solar day rotations of the earth. The extra 0.24 hours don’t “come out of nowhere.” That event doesn’t occur at the same moment every 365 solar says. It happens about 6 hours later every year.

And as Macharios says, (I think) the calendar we use for convention’s sake ignores those “extra hours” for a few years even though celestially the equinox is shifted. Rather than adjust yearly, incrementally, we let it go, accounting for those extra hours with a whole day adjustment every 4 years to realign. But the sun and earth don’t wait for man’s calendar. If we didn’t adjust, our calendars would fall behind because of those “extra hours” and after awhile, we’d notice the seasons weren’t right.

1133

Flat Earth Investigations / Re: Possible Issue with Solar Noon in Round Earth Theory

« on: April 25, 2018, 08:37:51 AM »

That link does not explain where the extra hours comes from. See The Problem post.

The “extra hours” aren’t “extra.” They’re just the difference between sidereal and solar references.

The Solar Day does not fit into the Solar Year. The Sidreal Day and the Sidreal Year have nothing to do with it.

I thought your problem was the 12 hour offset at the halfway mark of the earth’s orbit around the sun. That’s explained by the difference between sidereal and solar day references.

If sidereal has nothing to do with it, then what’s the problem again? “The solar day doesn’t fit into the solar year?” What does that mean? Are the “extra hours” you’re now talking about the 0.24 day tacked onto the 356 day solar year? That’s a different issue. A different problem.

Following your link to The Problem, I see you state “The sun needs to return back to the same position every year in a Solar Year.” It doesn’t “need to.” I know for the sake of tidiness it would be nice if it did. There’d be no need for leap days or leap years. But it doesn’t line up that neatly because it doesn’t “need to” just to make it easy for us. It’s close enough that we barely notice it at first, but the mismatch between solar day and solar year can add up over time, thus the need to “catch up” with leaps.

If those are the “extra hours” then yes. That IS different from what I’ve been trying to explain about the NYC half year “problem” you started with. Those ARE extra hours, needed BECAUSE the solar days don’t “fit” the solar year in a nice, whole number of 365. The earth, on that 365th solar day is coming up just a bit short from where it began, relative to the sun.

(Frankly, I wouldn’t worry about the sidereal year. That’s yet a whole ‘nuther ball of wax that, if having trouble with sidereal days versus solar days, and solar days fitting into solar years, it’ll only compound the confusion, and it isn’t necessary for resolving what you’ve been asking.)

1134

Flat Earth Investigations / Re: Possible Issue with Solar Noon in Round Earth Theory

« on: April 25, 2018, 08:07:43 AM »

That link does not explain where the extra hours comes from. See The Problem post.

The “extra hours” aren’t “extra.” They’re just the difference between sidereal and solar references.

1135

Flat Earth Investigations / Re: Possible Issue with Solar Noon in Round Earth Theory

« on: April 25, 2018, 08:03:07 AM »

There is something that seems wrong with the way the earth rotates around the Sun. Consider the following image that we are taught in school:




Assume that New York City is in its Solar Noon (look at where New York City is in the top and bottom September and March figures in the above illustration). After 6 months the motions suggests that New York City will be in darkness during its noontime.

I’d like to point out that, like the flat earth animation graphic, that picture you’ve chosen of earth’s orbit about the sun is just a visualization. It’s illustrating a point about tilt and equinox/solstice and isn’t meant to be a scale, accurate representation. The globe earth is a copy and paste icon massively larger and close to a tiny cartoon sun.

But, your question is understandable nonetheless...

Some Rough Calculations

Napkin Calculation 1

Day = 24 hours
Year = 365 days

365 days / 2 = 182.5 days in 6 months
24 hours x 182.5 days = 4380 hours in 6 months
4380 hours / 360 (since the sun rotates around the earth 360 degrees in one day) = 12.16666 hour offset

Earth should be offset by 12.16666 hours (similar to the above image)? NYC should be in night?

Yes. The approach you took is confusing, but the solar day and sidereal day will be offset by about 12 hours, and the side of the world facing the sun at the starting gun will be facing away from the sun at the halfway point.

Napkin Calculation 2

According to RET particulars, the earth doesn't rotate at exactly 24 hours a day, and the earth doesn't have an exactly 365 day year, which is why we have to change times and add a leap year every 4 years.

Sidreal Day = 23.933333 hours
Sidreal Year = 365.25636 days

365.25636 days per year / 2 = 182.62818 days in 6 months
23.933333 hours per day x 182.62818 days = 4370.90104712394 hours in 6 months
4370.90104712394  / 360 (since the sun rotates around the earth 360 degrees in one day) = 12.14139179 hours offset

Earth should be offset by 12.14139179 hours? NYC should be in night?

Again, don’t agree with the method, but same result: an “offset” as should be expected between a star field frame of reference and a solar frame of reference at the half yearly mark.

Napkin Calculation 3

Some sources say that the earth "actually" rotates 360.98 degrees per day.

360.98 degrees in a day x 182.62818 days in 6 months
= 65925.1204164 degrees in 6 months
ans / 360.98 = offset is 183.62818 degrees.

Earth should be offset by 183.62818 degrees? NYC should be in night?

--- --- ---

Corrections with the 360.98 figure

Using 360.98 degrees per day in the second calculation, replacing 360 with 360.98, gives an offset of 12.1082 hours. The offset still says that NYC should be in night.

Replacing 360 with 360.98 in the third calculation gives an offset answer of 182.625 degrees. The offset still says that NYC should be in night.

---

I may be going about this entirely wrong. Can I have some help with this seemingly glaring problem?

Even when cross mixing sidereal and synodic parameters, you’re still getting a affirmation that there’s about a half a day/half  a rotation delta between sidereal and solar. And yes, if NYC was at high noon at the start, it’ll be in darkness at half way around the orbit.

The fact that the earth orbits while it rotates is why.
Solar day is 24.000 hours per 360.986 degrees.
Sidereal day is 23.934 hrs per 360.000 degrees.
After halfway thru 365.24 solar days (which is also 366.24 sidereal days) the two measures will be offset by about 12 hours, which means it will be oriented the same as it was to the stars when it started the year but 180 degrees out in relation to the sun.

1136

Flat Earth Investigations / Re: Possible Issue with Solar Noon in Round Earth Theory

« on: April 25, 2018, 07:30:45 AM »

Yes, I am using Solar Days and Solar Years in the equation. I do not believe that I am mixing up terms. The Mean Solar Day has 24 hours and the Mean Solar Year has 365.24 years.

And so the number of degrees rotated in a solar day is what? Not 360. Which is what you’re using. But that’s a sidereal measure. Not solar because of the earth’s orbit means it needs to rotate just a bit more,

That number is 360.986 degrees. Use that per 24 hrs. Not 360.

Half way round the sun takes 182.62 days.
At an extra 0.986 degs of rotation a day, that’s 180 extra degrees. A half turn. So, if it was noon in NYC at the start of the solar year, it’ll be midnight when reaching the halfway point.

You don’t even need to get into the weeds for it to make sense. Rounding to 365 days in a year, half is 182.5.  0.5 of a 24 hour day is 12 hours. The “offset” makes sense. NYC will mark the halfway point in darkness if the clock started at noon NYC time.

In sidereal time, that’s when you use 360 degs because the sun is not the reference. You get the same result (NYC facing away from the sun at 1/2 year) but the clock isn’t synced to 360 degs per 24 hrs. It’s 360 degs per 23.934 hrs. And instead of 365.24 solar days, use 366.24 sidereal days. Halfway is 183.12 sidereal days. How much shorter are sidereal days? 3.93 minutes. So in 183.12 sidereal days, you lose about 12 hours compared to the solar day.

It adds up. The “offset” you were curious about and considered a problem is just the difference between sidereal and solar days, depending on what your reference point. If talking solar, count 24 hrs in a day, but account for the added degree of rotation in a solar day. If talking sidereal, use 360 degrees of rotation, but shorten the “day” parameter by 3 mins 56 secs. Figuring with 360 degrees (a sidereal measure) with 24 hours (a solar measure) is mixing terms.

1137

Flat Earth Investigations / Re: Possible Issue with Solar Noon in Round Earth Theory

« on: April 25, 2018, 01:13:16 AM »

Thank you. The difference is stated in these links:

From: http://astro.unl.edu/naap/motion3/sidereal_synodic.html

A sidereal year is the time it takes for the sun to return to the same position with respect to the stars. Due to the precession of the equinoxes the sidereal year is about 20 minutes longer than the tropical year.

That's the difference between a sidereal year and a solar (tropical year). Different from a sidereal day and solar day.

I understand the confusion, but you're mixing terms. (Not units of measurement; just terms.) There's a rotation of the earth (days) and there's orbital rotation (years). Each has a difference measurement based on whether sun is a reference point or a distant star field. The solar day is different from the sidereal day for one reason. The solar year is different from the sidereal year for others.

All I'm trying to say is make sure when doing your calculations you're using the same terms; convert if necessary, so that you're not dividing the time parameters into non-agreeing angular parameters. There are two "circles": earth's rotation and earth's orbit. If using sidereal for either, stick with the time intervals for sidereal angular displacement. If using solar, apply the solar time intervals. If relating the two, use proper conversion.

I haven't checked your math. I'm just noting confusion of terms/variables.

1138

Flat Earth Investigations / Re: Possible Issue with Solar Noon in Round Earth Theory

« on: April 25, 2018, 12:18:25 AM »

Per the Sidrael Day comment I refer you to this post which shows that the Sidrael Day is not the solution to this problem.

"If the stars did not exist the Solar Day is still wrong." - the stars are a reference point. If no reference point for 360° earth rotation, the earth would still have to rotate 360.986° to face the sun again (and we'd call that 24 hours). But without a reference point, we might be excused for thinking that we'd rotated 360° and divided those degrees into 24 hours. And we'd probably find it normal, maybe, that time of day would slip as we orbited the sun. Maybe, eventually, humans would figure it out that the 24 hours was dividing 360.986° and not 360° without the distant starfield to provide a reference. Who knows?

But you are right. If mankind continued to think 1 rotation of the earth was solar noon to solar noon, and that equated to 360°, then solar days would be "wrong," at least as we know them now. They probably wouldn't be "wrong" to a person in a no-stars world though. If they didn't adjust, they'd just adapt and accept that day/night shift during the year.


"The Sidrael Day is about 4 seconds less than the Solar Day."  - actual value is 3 mins, 56 secs. Rework your calculation using the correct delta.

1139

Flat Earth Investigations / Re: Possible Issue with Solar Noon in Round Earth Theory

« on: April 25, 2018, 12:03:40 AM »

You're cherry-picking your systems to only select those which fit your needs.

I'm sorry for butting in. I can't figure out what the argument is about. I thought I had my finger on the disconnect, but maybe not. Maybe you are arguing about numbers/units and not terms/variables.

I'll go back to lurk mode (after responding to Tom's suggestion I read his earlier post.)

1140

Flat Earth Investigations / Re: Possible Issue with Solar Noon in Round Earth Theory

« on: April 24, 2018, 11:59:31 PM »

You can mix terms. You can call the variables anything you want to call it...

"Terms" are not what you call them. "Terms" are the variables you are applying.

Sure, you can make up any standards or units of measurement you want for those terms, but whatever you use, you have to be clear on what it is you're working with. The ratio you are working with is either the degrees of earth's rotation to bring the same line back toward the sun in 24 hours, OR 360° of earth rotation per the time it takes to complete that rotation.

But you aren't working with the right terms if applying a ratio of numerator of one (360°) with the denominator of the other (24 hrs). Doing that results in the question you posed in the opening post. Keep the right degrees of rotation with the correct, corresponding time period. You can use whatever units of measurement for those terms you like.