[JSS]

We predicted Comet Shoemaker–Levy's multiple impacts with Jupiter over a year in advance using Newton's math. Explain how we did that if the math doesn't work?

That was discussed in the other thread on that matter. They only predicted a portion of an orbit, and are using other methods such as epicycles.

Yes it was, and it was pointed out they predicted nearly a full orbit, and papers were linked that clearly stated they used Newtons methods not 'epicycles'.

Epicycles wouldn't work anyway as the final orbit was bent inward toward Jupiter as it got closer.

The simple fact is the math WORKS. I have to believe actual predictions over one persons insistence that it doesn't.

[Tom Bishop]

We predicted Comet Shoemaker–Levy's multiple impacts with Jupiter over a year in advance using Newton's math. Explain how we did that if the math doesn't work?

That was discussed in the other thread on that matter. They only predicted a portion of an orbit, and are using other methods such as epicycles.

Yes it was, and it was pointed out they predicted nearly a full orbit, and papers were linked that clearly stated they used Newtons methods not 'epicycles'.

Epicycles wouldn't work anyway as the final orbit was bent inward toward Jupiter as it got closer.

The simple fact is the math WORKS. I have to believe actual predictions over one persons insistence that it doesn't.

No, those papers said that they were using perturbation methods, which are epicycles which use a two body problem as the underlying model instead of Ptolmy's circle. You have not yet provided a rebuttal with appropriate sources to the sources given explaining this.

[JSS]

We predicted Comet Shoemaker–Levy's multiple impacts with Jupiter over a year in advance using Newton's math. Explain how we did that if the math doesn't work?

That was discussed in the other thread on that matter. They only predicted a portion of an orbit, and are using other methods such as epicycles.

Yes it was, and it was pointed out they predicted nearly a full orbit, and papers were linked that clearly stated they used Newtons methods not 'epicycles'.

Epicycles wouldn't work anyway as the final orbit was bent inward toward Jupiter as it got closer.

The simple fact is the math WORKS. I have to believe actual predictions over one persons insistence that it doesn't.

No, those papers said that they were using perturbation methods, which are epicycles which use a two body problem as the underlying model instead of Ptolmy's circle. You have not yet provided a rebuttal with appropriate sources to the sources given explaining this.

Yes, they were using models based on Newtons 2-body equations. Which is exactly how one uses Newton's laws to calculate orbits. Perturbation methods are a very well known and often used method for solving complex math. Especially with the advent of computers that allows huge numbers of calculations to be run to as much precision as you need.

https://en.wikipedia.org/wiki/Perturbation_theory

So as you stated, they used Newtons 2-body formulas combined with Perturbation theory to correctly predict a series of comet collisions.  Seems like Newton's math works.

[Tom Bishop]

From your article we see:

Perturbation theory was first devised to solve otherwise intractable problems (links us to the Three Body Problem page) in the calculation of the motions of planets in the solar system. For instance, Newton's law of universal gravitation explained the gravitation between two astronomical bodies, but when a third body is added, the problem was, "How does each body pull on each?" Newton's equation only allowed the mass of two bodies to be analyzed. The gradually increasing accuracy of astronomical observations led to incremental demands in the accuracy of solutions to Newton's gravitational equations, which led several notable 18th and 19th century mathematicians, such as Lagrange and Laplace, to extend and generalize the methods of perturbation theory.

From the same article, see bolded:

Perturbation theory is closely related to methods used in numerical analysis. The earliest use of what would now be called perturbation theory was to deal with the otherwise unsolvable mathematical problems of celestial mechanics: for example the orbit of the Moon, which moves noticeably differently from a simple Keplerian ellipse because of the competing gravitation of the Earth and the Sun.[2]

Perturbation methods start with a simplified form of the original problem, which is simple enough to be solved exactly. In celestial mechanics, this is usually a Keplerian ellipse. Under non-relativistic gravity, an ellipse is exactly correct when there are only two gravitating bodies (say, the Earth and the Moon) but not quite correct when there are three or more objects (say, the Earth, Moon, Sun, and the rest of the solar system) and not quite correct when the gravitational interaction is stated using formulations from General relativity.

It's a work around for otherwise unsolvable mathematical problems of celestial mechanics.

How is it that they can't simulate three bodies, but they have a work around which involves computing the effects bodies have on each other?

Physcist Dr. Gopi Krishna Vijaya says that, in using Perturbation Theory, astronomers are really using epicycles with a gravitational disguise.

Replacing the Foundations of Astronomy - .pdf

Epicycles Once More

“ Following the Newtonian era, in the 18th century there were a series of mathematicians – Bernoulli, Clairaut, Euler, D’Alembert, Lagrange, Laplace, Leverrier – who basically picked up where Newton left off and ran with it. There were no descendants to the wholistic viewpoints of Tycho and Kepler, but only those who made several improvements of a mathematical nature to Newtonian theory. Calculus became a powerful tool in calculating the effects of gravitation of all the planets upon each other, due to their assumed masses. The motion of the nearest neighbor – the Moon – was a surprisingly hard nut to crack even for Newton, and several new mathematical techniques had to be invented just to tackle that.

In the process, a new form of theory became popular: Perturbation theory. In this approach, a small approximate deviation from Newton's law is assumed, based on empirical data, and then a rigorous calculation of differential equation is used to nail down the actual value of the deviation. It does not take much to recognize that this was simply the approach taken before Kepler by Copernicus and others for over a thousand years – adding epicycles to make the observations fit. It is the same concept, but now dressed up in gravitational disguise: ”



“ In other words, the entire thought process took several steps backwards, to redo the same process as the Ptolemaic - Copernican epicycle theory, only with different variables. The more logical way of approach would have been to redirect the focus of the improved mathematical techniques to the assumptions in Newton’s theory, but instead the same equations were re-derived with calculus, without examining the assumptions. Hence any modern day textbook gives the same derivation for circular and elliptical motion that Newton first derived in his Principia. The equivalence of the epicycle theory and gravitational theory has not been realized, and any new discovery that fits in with the mathematical framework of Newtonian gravity is lauded as a “triumph of the theory of gravitation.” In reality, it is simply the triumph of fitting curves to the data or minor linear extrapolations – something that had already been done at least since 2nd century AD. Yet the situation is conceptually identical. ”

Celestial Mechanics Professor Charles Lane Poor said:

The deviations from the “ideal” in the elements of a planet’s orbit are called “perturbations” or “variations”.... In calculating the perturbations, the mathematician is forced to adopt the old device of Hipparchus, the discredited and discarded epicycle. It is true that the name, epicycle, is no longer used, and that one may hunt in vain through astronomical text-books for the slightest hint of the present day use of this device, which in the popular mind is connected with absurd and fantastic theories. The physicist and the mathematician now speak of harmonic motion, of Fourier’s series, of the development of a function into a series of sines and cosines. The name has been changed, but the essentials of the device remain. And the essential, the fundamental point of the device, under whatever name it may be concealed, is the representation of an irregular motion as the combination of a number of simple, uniform circular motions.

We saw earlier from your source that the actual way, The Three Body Problem, the real dynamical system under Newton's laws, doesn't work.

[JSS]

It's a work around for otherwise unsolvable mathematical problems of celestial mechanics.

How is it that they can't simulate three bodies, but they can have this work around to accurately compute the bodies?

Easily. When you can't solve an algebraic set of equations, you use other methods to approximate to however high a degree as you need.  Numeric integration is a commonly used method in physics and math in general. You can't use PI directly in the real world, but you can use a numeric approximation.

Numerical analysis continues this long tradition: rather than exact symbolic answers, which can only be applied to real-world measurements by translation into digits, it gives approximate solutions within specified error bounds. - https://en.wikipedia.org/wiki/Numerical_analysis

[Tom Bishop]

Ptolmy used numerical procedures in the Almagest too. What makes you think that these numerical procedures using sines and cosines and fourier methods for perturbation analysis aren't talking about epicycles?

https://books.google.com/books?id=JVhTtVA2zr8C&pg=PA29&source=gbs_toc_r&cad=4#v=onepage&q&f=false

[JSS]

Ptolmy used numerical procedures in the Almagest too. What makes you think that these numerical procedures using sines and cosines and fourier methods for perturbation analysis aren't talking about epicycles?

https://books.google.com/books?id=JVhTtVA2zr8C&pg=PA29&source=gbs_toc_r&cad=4#v=onepage&q&f=false

Yes, numerical methods are a very old technique. There is nothing wrong with using it, it's how we convert pure math into actual numbers without solving exact equations.

The numerical point of view goes back to the earliest mathematical writings. A tablet from the Yale Babylonian Collection (YBC 7289), gives a sexagesimal numerical approximation of the square root of 2, the length of the diagonal in a unit square. - https://en.wikipedia.org/wiki/Numerical_analysis

From https://en.wikipedia.org/wiki/Deferent_and_epicycle ...

Newtonian or classical mechanics eliminated the need for deferent/epicycle methods altogether and produced more accurate theories. By treating the Sun and planets as point masses and using Newton's law of universal gravitation, equations of motion were derived that could be solved by various means to compute predictions of planetary orbital velocities and positions. Simple two-body problems, for example, can be solved analytically. More-complex n-body problems require numerical methods for solution.

The power of Newtonian mechanics to solve problems in orbital mechanics is illustrated by the discovery of Neptune. Analysis of observed perturbations in the orbit of Uranus produced estimates of the suspected planet's position within a degree of where it was found. This could not have been accomplished with deferent/epicycle methods.

That said, epicycles are not some sort of poision. If an astronomer uses one it's because he's decided it's good enough for the result he needs. We have a large numbers of mathematical tools at our disposal, and use whichever best fits our needs. Be it accuracy or speed or ease of understanding the problem.

[Tom Bishop]

Perturbation Theory not really that legitimate, and is the backwards way of doing science by starting with the solution and building corrections from the ideal state (like Ptolmy did with his epicycles - he started with the observation and his "perfect" model and built corrections to match it with epicycles). It says as much on the Discovery of Neptune page: https://en.wikipedia.org/wiki/Discovery_of_Neptune

Adams learned of the irregularities while still an undergraduate and became convinced of the "perturbation" hypothesis.

...In modern terms, the problem is an inverse problem, an attempt to deduce the parameters of a mathematical model from observed data.

This is, of course, exactly opposite of using a mathematical model to predict.

That is what Dr. Gopi Krishna Vijaya explained what was happening. They 'fit' data to observations with a series of corrections.

The Wikipedia article on Perturbation Theory:

This general procedure is a widely used mathematical tool in advanced sciences and engineering: start with a simplified problem and gradually add corrections that make the formula that the corrected problem becomes a closer and closer match to the original formula.

The book Approximate Analytical Methods for Solving Ordinary Differential Equations states on p.65:

The perturbation theory had its roots in early studies of celestial mechanics, for which the theory of epicycles was used to make small corrections to the prediction of the path of planets. Later, Charles Eugene used it to study the solar system, in particular the earth-sun- moon system. Now, it finds applications in many f‌ields, such as f‌luid dynamics, quantum mechanics, quantum chemistry, quantum f‌ield theory, and so on.

The idea behind the perturbation method is that we start with a simplif‌ied form of the original problem (which may be extremely diff‌icult to handle) and then gradually add corrections or perturbations, so that the solution matches that of the original problem. The simplif‌ied form is obtained by letting the perturbation parameter take the zero value.

What they were doing is mapping out all of the corrections that they had to make to Uranus and deducing that "these corrections are cause by Jupiter" and "these corrections are from x," etc. The models used tend to have hundreds and thousands of corrections/perturbations. They found odd a buildup irregularities from the corrections and concluded that it was from another planet.

---

Also, the claimed Discovery of Neptune success of Perturbation Theory was discredited by some, who declared that they had only discovered Neptune by luck.

From Earthsky.org - https://earthsky.org/human-world/today-in-science-discovery-of-neptune

Ironically, as it turns out, both Le Verrier and Adams had been very lucky. Their predictions indicated Neptune’s distance correctly around 1840-1850. Had they made their calculations at another time, both predicted positions would have been off. Their calculations would have predicted the planet’s position only 165 years later or earlier, since Neptune takes 165 years to orbit once around the sun.

By the way, Neptune might have been discovered without the aid of mathematics. Like all planets in our solar system – because it’s closer to us than the stars – it can be seen from Earth to move apart from the star background. For example, the great astronomer Galileo, using one of the first telescopes, is said to have recorded Neptune as a faint star in 1612. If it had watched it over several weeks, he’d have noticed its unusual motion.

http://www.helas.gr/conf/2011/posters/S_5/dallas.pdf

Airy seems to be the only scientist involved in the discovery that has thoughts of a possible modification of Newtonian gravity to explain the irregular movement of Uranus. But nowhere in his memoire is there a statement that the discovery of Neptune is a test, let alone a critical one, of the law of gravitation. It was apparent shortly after the discovery that luck played its part in the easy discovery of Neptune. The whole process is extremely error prone, in both the calculations and the observations, so if the planet were not discovered in the circumstances of 1846, this would not be a refutation of Newtonian gravity, but simply a refutation of the auxiliary prepositions.

See the following from astronomer Sears C. Walker:

If we admit for the moment that my views are correct, then LeVerrier's announcement of March 29th is in perfect accordance with that of Professor Peirce of the 16th of the same month, viz. that the present visible planet Neptune is not the mathematical planet to which theory had directed the telescope. None of its elements conform to the theoretical limits. Nor does it perform the functions on which alone its existence was predicted, viz. those of removing that opprobrium of astronomers, the unexplained perturbations of Uranus.

We have it on the authority of Professor Peirce that if we ascribe to Neptune a mass of three-fourths of the amount predicted by LeVerrier, it will have the best possible effect in reducing the residual perturbations of Uranus below their former value; but will nevertheless leave them on the average two-thirds as great as before.

It is indeed remarkable that the two distinguished European astronomers, LeVerrier and Adams, should, by a wrong hypothesis, have been led to a right conclusion respecting the actual position of a planet in the heavens. It required for their success a compensation of errors. The unforeseen error of sixty years in their assumed period was compensated by the other unforeseen error of their assumed office of the planet. If both of them had committed only one theoretical error, (not then, but now believed to be such,) they would, according to Prof. Peirce's computations, have agreed in pointing the telescope in the wrong direction, and Neptune might have been unknown for years to come.

[JSS]

What you posted about Neptune verifies that Perturbation Theory not legitimate, and is the backwards way of doing science by starting with the solution and building corrections from the ideal state.

It says as much on the Discovery of Neptune page: https://en.wikipedia.org/wiki/Discovery_of_Neptune

In modern terms, the problem is an inverse problem, an attempt to deduce the parameters of a mathematical model from observed data.

What they were doing is mapping out all of the corrections that they had to make to Uranus and guessing that "these epicycles are cause by Jupiter" and "these epicycles are from x," etc. The models used have thousands of perturbations (epicycles).

How is that backwards? They had observations that included anomalies, came up with a hypothesis that something big must be out there causing them, turned it into a theory that predicted where it must be and then found it.  Classic science. They also got lucky, also well established in science. But that luck only worked because they did know where to look, just not when. The orbit was still correct.

Further, the success of Perturbation Theory and Gravitation was later discredited.

...

So not everyone agreed that this claim is a proof of anything.

As many things are, we can argue this one round and round. Nothing in any of those quotes "discredits Perturbation Theory and Gravitation". At most it throws doubt onto how accurate the discovery of Neptune was. It certainly doesn't suggest as you do that it somehow totally invalidates Perturbation Theory. That's an entire branch of math which orbital mechanics is just one small use case, and thousands of mathematicians would want to have words with you if you tried to claim it was 'discredited'.

Even your quote says as much - The whole process is extremely error prone, in both the calculations and the observations, so if the planet were not discovered in the circumstances of 1846, this would not be a refutation of Newtonian gravity, but simply a refutation of the auxiliary prepositions

Perturbation Theory is extremely well established math, and none of those articles even hints it's even slightly wrong.

Read the entire wiki page about it, nowhere does it say it's discredited - https://en.wikipedia.org/wiki/Perturbation_theory

[Tom Bishop]

The above quotes state that Neptune was discovered by luck, rather than the accuracy or reliability of the mathematical model.

Science historian Nicholas Kollerstrom also states that dishonesty was involved with this claim.

https://en.m.wikipedia.org/wiki/Discovery_of_Neptune

In an interview in 2003, historian Nicholas Kollerstrom concluded that Adams's claim to Neptune was far weaker than had been suggested, as he had vacillated repeatedly over the planet's exact location, with estimates ranging across 20 degrees of arc. Airy's role as the hidebound superior willfully ignoring the upstart young intellect was, according to Kollerstrom, largely constructed after the planet was found, in order to boost Adams's, and therefore Britain's, credit for the discovery.

The planets are all following a path called the ecliptic, and aren't randomly distributed in the sky. 20 degrees of arc? Really?


LeVerrier later went on to "discover" the planet Vulcan with his same perturbation methods. - http://adsabs.harvard.edu/full/1953ASPL....6..291E

One of the most intemfing stories in astronomy
concerns the history of what was once believed
to be an intra-mercurial planet—Vulcan. The story
begins in 1859 when the planet was “discovered’
by Urbain Jean Joseph Leverrier.

Leverrier was born on March 11, 1811, the son
of a French civil servant. His birthplace, Saint
L6, is now familiar to most of us as the place
where the allies “broke out” after the Normandy
landings in the last world war.

Jean Leverrier introduced a new concept into
planetary discovery. As he was a mathematical,
rather than an observational astronomer, there is
some basis for the belief that he never looked
through a telescope. He discovered planets while
seated at his desk in the Ecole Polytechnique in
Paris. His first discovery was Neptune; his second
was Vulcan.

We all know how that one turned out.

[JSS]

The above quotes state that Neptune was discovered by luck, rather than the accuracy or reliability of the mathematical model.

The planets are all following a path called the Ecliptic, and aren't randomly distributed in the sky. This isn't some amazing thing.

Also, LeVerrier later went on to "discover" the planet Vulcan with his same perturbation methods. - http://adsabs.harvard.edu/full/1953ASPL....6..291E

The planet Vulcan is interesting. Yet again showing how well science works. People noticed Mercury was slightly off in it's orbit and there were numerous theories proposed. One of these was suggesting a planet Vulcan could be causing it in the 1850's. Then another theory proposed a solution half a century later, Einstein's theory of relativity. This did fit the observations perfectly, and thus once again science worked. Several theories were developed and one was eventually shown to be correct.

Now that WAS down purely to the reliability of the mathematical model. Einsteins theory is so well tested and successful that we have yet to prove it off in any way. Every test, even measuring how space-time twists around rotating objects has been tested and matches just what we would expect.

Vulcan's a great success story.

[Tom Bishop]

The above quotes state that Neptune was discovered by luck, rather than the accuracy or reliability of the mathematical model.

The planets are all following a path called the Ecliptic, and aren't randomly distributed in the sky. This isn't some amazing thing.

Also, LeVerrier later went on to "discover" the planet Vulcan with his same perturbation methods. - http://adsabs.harvard.edu/full/1953ASPL....6..291E

The planet Vulcan is interesting. Yet again showing how well science works. People noticed Mercury was slightly off in it's orbit and there were numerous theories proposed. One of these was suggesting a planet Vulcan could be causing it in the 1850's. Then another theory proposed a solution half a century later, Einstein's theory of relativity. This did fit the observations perfectly, and thus once again science worked. Several theories were developed and one was eventually shown to be correct.

Now that WAS down purely to the reliability of the mathematical model. Einsteins theory is so well tested and successful that we have yet to prove it off in any way. Every test, even measuring how space-time twists around rotating objects has been tested and matches just what we would expect.

Vulcan's a great success story.

Quite the contrary, it shows that Perturbation Theory predictions are really a guessing game. Hypothesizing the existence of undiscovered planets based on perceived irregularities rather than mathematical certainty.


As for Einstein, not everyone agreed with that one either:

Relativity and the Motion of Mercury
Charles Lane Poor, Ph.D.
Professor Emeritus of Celestial Mechanics,
Columbia University

Link to Paper. From the Introduction:   

“ Does the relativity theory, as asserted by Einstein, explain and account for even the single motion of tile perihelion of Mercury? In what way do the formulas of relativity differ from those of the classical mathematics of Newton, and how do these new formulas explain this motion? It is the purpose of this paper to discuss this single phase of the matter; to show that the very equations, or formulas, cited by the relativists as furnishing an explanation of this motion, utterly fail to furnish such an explanation. The formulas of relativity dynamics can not and do not explain the observed perihelial motion of Mercury. ”

The Theory of Mercury’s Anomalous Precession
Roger A. Rydin, Sc.D.
Associate Professor Emeritus of Nuclear Engineering,
University of Virginia
Link to Paper

Abstract:   “ Urbain Le Verrier published a preliminary paper in 1841 on the Theory of Mercury, and a definitive paper in 1859. He discovered a small unexplained shift in the perihelion of Mercury of 39” per century. The results were corrected in 1895 by Simon Newcomb, who increased the anomalous shift by about 10%. Albert Einstein, at the end of his 1916 paper on General Relativity, gave a specific solution for the perihelion shift which exactly matched the discrepancy. Dating from the 1947 Clemence review paper, that explanation and precise value have remained to the present time, being completely accepted by theoretical physicists as absolutely true. Modern numerical fittings of planetary orbits called Ephemerides contain linearized General Relativity corrections that cannot be turned off to see if discrepancies between observation and computation still exist of the magnitude necessary to support the General Relativity estimates of the differences.

The highly technical 1859 Le Verrier paper was written in French. The partial translation given here throws light on Le Verrier’s analysis and thought processes, and points out that the masses he used for Earth and Mercury are quite different from present day values. A 1924 paper by a professor of Celestial Mechanics critiques both the Einstein and the Le Verrier analyses, and a 1993 paper gives a different and better fit to some of Le Verrier’s data. Nonetheless, the effect of errors in planet masses seems to give new condition equations that do not change the perihelion discrepancy by a large amount. The question now is whether or not the excess shift of the perihelion of Mercury is real and has been properly explained in terms of General Relativity, or if there are other reasons for the observations. There are significant arguments that General Relativity has not been proven experimentally, and that it contains mathematical errors that invalidate its predictions. Vankov has analyzed Einstein’s 1915 derivation and concludes that when an inconsistency is corrected, there is no perihelion shift at all! ”

Einstein’s Explanation of Perihelion Motion of Mercury
Hua Di
Academician, Russian Academy of Cosmonautics
Research Fellow (ret.), Stanford University

From Unsolved Problems in Special and General Relativity

p.7

  “ Einstein’s general theory of relativity cannot explain Mercury’s perihelion motion. He obtained “for the planet Mercury, a perihelion advance of 43” per century” by an incorrect integral calculus and many arbitrary approximations. His formula (1) is a poorly patched wrong result, tailored specially for Mercury. That is why his formula (1) fails to explain the perihelion motions for Earth and Mars. Einstein was unfair to blame “the small eccentricities of the orbits of these planets” for his failure. To sum up, Einstein’s general theory of relativity is dubious. ”

[JSS]

The above quotes state that Neptune was discovered by luck, rather than the accuracy or reliability of the mathematical model.

The planets are all following a path called the Ecliptic, and aren't randomly distributed in the sky. This isn't some amazing thing.

Also, LeVerrier later went on to "discover" the planet Vulcan with his same perturbation methods. - http://adsabs.harvard.edu/full/1953ASPL....6..291E

The planet Vulcan is interesting. Yet again showing how well science works. People noticed Mercury was slightly off in it's orbit and there were numerous theories proposed. One of these was suggesting a planet Vulcan could be causing it in the 1850's. Then another theory proposed a solution half a century later, Einstein's theory of relativity. This did fit the observations perfectly, and thus once again science worked. Several theories were developed and one was eventually shown to be correct.

Now that WAS down purely to the reliability of the mathematical model. Einsteins theory is so well tested and successful that we have yet to prove it off in any way. Every test, even measuring how space-time twists around rotating objects has been tested and matches just what we would expect.

Vulcan's a great success story.

Quite the contrary, it shows that Perturbation Theory predictions are really a guessing game. Hypothesizing the existence of undiscovered planets based on perceived irregularities rather than mathematical certainty.

This is how science works. You have data, you try and explain it by making guesses and hypothesis and then you TEST to find out if your hypothesis stands up or not. Then you have a theory. In the real world you don't always have perfect data and NOTHING is ever a mathematical certainty.

If we never guessed or imagined, never looked under rocks or in shadows then we would still be stumbling around in caves.

As for Einstein, not everyone agreed with that one either:

If there was any evidence Einstein was wrong it would be massive news. It's the most tested and proven theory we have, perhaps with the exception of Quantum Mechanics. Your references are all flawed.

Relativity and the Motion of Mercury
Charles Lane Poor, Ph.D.
Professor Emeritus of Celestial Mechanics,
Columbia University

Link to Paper. From the Introduction:   

“ Does the relativity theory, as asserted by Einstein, explain and account for even the single motion of tile perihelion of Mercury? In what way do the formulas of relativity differ from those of the classical mathematics of Newton, and how do these new formulas explain this motion? It is the purpose of this paper to discuss this single phase of the matter; to show that the very equations, or formulas, cited by the relativists as furnishing an explanation of this motion, utterly fail to furnish such an explanation. The formulas of relativity dynamics can not and do not explain the observed perihelial motion of Mercury. ”

This is from 1925. We have since proven Einstein right beyond a doubt with much better measurements and countless experiments.

The Theory of Mercury’s Anomalous Precession
Roger A. Rydin, Sc.D.
Associate Professor Emeritus of Nuclear Engineering,
University of Virginia
Link to Paper

Abstract:   “ Urbain Le Verrier published a preliminary paper in 1841 on the Theory of Mercury, and a definitive paper in 1859. He discovered a small unexplained shift in the perihelion of Mercury of 39” per century. The results were corrected in 1895 by Simon Newcomb, who increased the anomalous shift by about 10%. Albert Einstein, at the end of his 1916 paper on General Relativity, gave a specific solution for the perihelion shift which exactly matched the discrepancy. Dating from the 1947 Clemence review paper, that explanation and precise value have remained to the present time, being completely accepted by theoretical physicists as absolutely true. Modern numerical fittings of planetary orbits called Ephemerides contain linearized General Relativity corrections that cannot be turned off to see if discrepancies between observation and computation still exist of the magnitude necessary to support the General Relativity estimates of the differences.

The highly technical 1859 Le Verrier paper was written in French. The partial translation given here throws light on Le Verrier’s analysis and thought processes, and points out that the masses he used for Earth and Mercury are quite different from present day values. A 1924 paper by a professor of Celestial Mechanics critiques both the Einstein and the Le Verrier analyses, and a 1993 paper gives a different and better fit to some of Le Verrier’s data. Nonetheless, the effect of errors in planet masses seems to give new condition equations that do not change the perihelion discrepancy by a large amount. The question now is whether or not the excess shift of the perihelion of Mercury is real and has been properly explained in terms of General Relativity, or if there are other reasons for the observations. There are significant arguments that General Relativity has not been proven experimentally, and that it contains mathematical errors that invalidate its predictions. Vankov has analyzed Einstein’s 1915 derivation and concludes that when an inconsistency is corrected, there is no perihelion shift at all! ”

This paper has a grand total of two citations, and none of those papers are refereed to by anyone else.  This is pretty much a dead paper, and if it proved Einstein wrong or even threw serious doubt then it would be referenced and discussed all over.  Poking holes in Relativity is one of science's Holy Grails after all and this would be front page science news if it could show just the hint of a crack.

Einstein’s Explanation of Perihelion Motion of Mercury
Hua Di
Academician, Russian Academy of Cosmonautics
Research Fellow (ret.), Stanford University

From Unsolved Problems in Special and General Relativity

p.7

  “ Einstein’s general theory of relativity cannot explain Mercury’s perihelion motion. He obtained “for the planet Mercury, a perihelion advance of 43” per century” by an incorrect integral calculus and many arbitrary approximations. His formula (1) is a poorly patched wrong result, tailored specially for Mercury. That is why his formula (1) fails to explain the perihelion motions for Earth and Mars. Einstein was unfair to blame “the small eccentricities of the orbits of these planets” for his failure. To sum up, Einstein’s general theory of relativity is dubious. ”

This isn't a paper, it's a book.  The quote you are referencing is from something called "Einstein’s Explanation of Perihelion Motion of Mercury" by Hua Di which seems to only exist in this book, as I can't find it published anywhere and every reference leads back to this book.

Not a proper reference.

[AATW]

Also, the claimed Discovery of Neptune success of Perturbation Theory was discredited by some, who declared that they had only discovered Neptune by luck.

From what I understand there was an element of luck in that Neptune happened to be in a point in its orbit where it was affecting the orbit of Uranus in such a way that they predicted something was "out there". The something ended up being Neptune.
The 'n' body problem is solved by splitting it into a series of 2 body problems. Ultimately the test of the model is whether it yields accurate results. And it demonstrably does. We were able to predict the path of the solar eclipse in 2017 to the block level. We have sent craft to Mars and Pluto and landed one on a meteor because our models of the solar system are good enough that we can do that.

Your issue seems to be that our model isn't perfect, which is true. But it's demonstrably good enough to be useful.

[Tom Bishop]

This is from 1925.

Einstein's theory is older than that. What's your point? As far as I can see Charles Lane Poor was a Professor of Celestial Mechanics and Einstein was not, which is a more direct authority on Mercury than a theoretical physicist.

This paper has a grand total of two citations, and none of those papers are refereed to by anyone else.

Actually I see that this modern paper cites Charles Lane Poor's work, who you rejected for being 'too old'. Also, much of Einstein's work went uncited. That's not a gauge for the validity or invalidity of a work.

This isn't a paper, it's a book.

It's a collection of papers published in a book. That seems like a weak argument.

We have since proven Einstein right beyond a doubt with much better measurements and countless experiments.

That's not true at all. Einstein was highly disputed, which is why he did not win the Nobel Prize for relativity, and was only awarded one for his work on the photoelectric effect, to which he responded by claiming racism.

...

Also, I found the current model of the Moon in the paper that stack posted.

See the illustration on page 600 and the caption, that the basic model was "adopted ever since."

V. THE MANY MOTIONS OF THE MOON

A. The traditional model of the Moon

A plane through the center of the Earth is determined at an inclination g of about 5 degrees with respect to the ecliptic. The Moon moves around the Earth in that plane on an ellipse with fixed semi-major axis a and eccentricity « of about 1/18. The Greek model was quite similar, except that the ellipse was replaced by an eccentric circle.

The plane itself rotates once every 18 years in the backward direction, i.e., against the prevailing motion in the solar system, while keeping its inclination constant. The perigee of the Moon, its point of closest approach to the Earth, makes a complete turn in the forward direction in about nine years.

The following picture (see Fig. 1) emerges: first we fix the direction of the spring equinox or some fixed star near it as the universal reference Q in the ecliptic: counting always from west to east, we determine the angle h from Q to the ascending node, i.e., the line of intersection for the Moon’s orbit with the ecliptic where the Moon enters the upper side of the ecliptic; from there we move by an angle g in the Moon’s orbital plane until we meet the perigee of the Moon; and finally we get to the Moon by moving through the true anomaly f. All these three angles have a double time dependence: linear (increasing for f and g, while decreasing for h) plus various periodic terms that average to 0.



~

D. The evection—Greek science versus Babylonian astrology

The Babylonians knew that the full moons could be as much as 10 hours early or 10 hours late; this is due to the eccentricity of the Moon’s orbit. But the Greeks wanted to know whether the Moon displays the same kind of speedups and delays in the half moons, either waxing or waning. The answer is found with the help of a simple instrument that measures the angle between the Moon and the Sun as seen from the Earth. The half moons can be as much as 15 hours early or late. With the Moon moving at an average speed of slightly more than 308 per hour (its own apparent diameter!), it may be as much as 5° ahead or behind in the new/full moons; but in the half moons, it may be as much as 7°308 ahead or behind its average motion. This new feature is known as evection.

Ptolemy found a mechanical analog for this peculiar complication, called the crank model. It describes the angular coupling between Sun and Moon correctly, but it has the absurd consequence of causing the distance of the Moon from the Earth to vary by almost a factor of 2. In the thirteenth century Hulagu Khan, a grandson of Genghis Khan, asked his vizier, the Persian all-round genius Nasir ed-din al Tusi, to build a magnificent observatory in Meragha, Persia, and write up what was known in astronomy at that time. Ptolemy’s explanation of the evection was revised in the process. In the fourteenth century Levi ben Gerson of Avignon in southern France seems to have been the first astronomer to measure the apparent diameter of the Moon (see Goldstein, 1972, 1997). Shortly thereafter Ibn al-Shatir of Damascus in Syria proposed a model for the Moon’s motion that coincides with the theory of Copernicus two centuries later. The crank model was replaced by two additional epicycles, yielding a more elaborate Fourier expansion in our modern terminology (see Swerdlow and Neugebauer, 1984).

With the improvements of the Persian, Jewish, and Arab astronomers, as well as Copernicus, the changes in the Moon’s apparent diameter are still too large with +/- 10%. As in Kepler’s second law, the Fourier expansion (12) has to include epicycles both in the backward and in the forward direction, in the ratio 3:1.

"The crank model was replaced by two additional epicycles, yielding a more elaborate Fourier expansion in our modern terminology."

"With the improvements of the Persian, Jewish, and Arab astronomers, as well as Copernicus, the changes in the Moon’s apparent diameter are still too large with +/- 10%. As in Kepler’s second law, the Fourier expansion (12) has to include epicycles both in the backward and in the forward direction, in the ratio 3:1."

[rabinoz]

We have since proven Einstein right beyond a doubt with much better measurements and countless experiments.

That's not true at all. Einstein was highly disputed, which is why he did not win the Nobel Prize for relativity, and was only awarded one for his work on the photoelectric effect, to which he responded by claiming racism.

JSS wrote "We have since proven Einstein right beyond a doubt with much better measurements and countless experiments."
But all you say is "Einstein was highly disputed" which does not refute the statement made by LSS in the slightest.
It is true that originally "Einstein was highly disputed" but since 1915 Einstein's General Theory of Relativity has gained almost, but not quite, universal acceptance.

There is now voluminous experimental evidence supporting GRT. for example:
Experimental Tests of General Relativity by Slava G. Turyshev

Why Relativity's True: The Evidence for Einstein's Theory[/b]]Why Relativity's True: The Evidence for Einstein's Theory
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Never stop testing
Even with all that evidence, we continue to put general relativity to the test. Any sign of a crack in Einstein's magnificent work would spark the development of a new theory of gravity, perhaps paving the way to uncovering the full quantum nature of that force. That's something we currently don't understand at all.

But in all regards, GR passes with flying colors; from sensitive satellites to gravitational lensing, from the [urlhttps://www.space.com/37745-einstein-relativity-tested-by-star-black-hole.html]orbits of stars[/url] around giant black holes to ripples of gravitational waves and the evolution of the universe itself, Einstein's legacy is likely to persist for quite some time.

Not that anyone regards Einstein's theories as the be all and end all.

Also, I found the current model of the Moon in the paper that stack posted.

See the illustration on page 600 and the caption, that the basic model was "adopted ever since."

That illustration might be but the current lunar orbit is no longer described in terms of an epicycle and different (with possibly an equant) but as an approximate precessing ellipse.

V. THE MANY MOTIONS OF THE MOON

A. The traditional model of the Moon

A plane through the center of the Earth is determined at an inclination g of about 5 degrees with respect to the ecliptic. The Moon moves around the Earth in that plane on an ellipse with fixed semi-major axis a and eccentricity « of about 1/18. The Greek model was quite similar, except that the ellipse was replaced by an eccentric circle.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
D. The evection—Greek science versus Babylonian astrology

The Babylonians knew that the full moons could be as much as 10 hours early or 10 hours late; this is due to the eccentricity of the Moon’s orbit. But the Greeks wanted to know whether the Moon displays the same kind of speedups and delays in the half moons, either waxing or waning. The answer is found with the help of a simple instrument that measures the angle between the Moon and the Sun as seen from the Earth. The half moons can be as much as 15 hours early or late. With the Moon moving at an average speed of slightly more than 308 per hour (its own apparent diameter!), it may be as much as 5° ahead or behind in the new/full moons; but in the half moons, it may be as much as 7°308 ahead or behind its average motion. This new feature is known as election.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
"With the improvements of the Persian, Jewish, and Arab astronomers, as well as Copernicus, the changes in the Moon’s apparent diameter are still too large with +/- 10%. As in Kepler’s second law, the Fourier expansion (12) has to include epicycles both in the backward and in the forward direction, in the ratio 3:1."

But all you include in your quote is "V. The traditional model of the Moon" and ignore the rest:
"VI. Newton’s Work in Lunar Theory",
"VII. Lunar Theory in the Age of Enlightenment",
"VIII. The Systematic Development of Lunar Theory",
"IX. The Canonical Formalism",
"X. Expansion around a Periodic Orbit" and most importantly
"XI. Lunar Theory in the 20th Century".

And soon after Newton published his "Laws of Motion and Universal Gravitation" Newton and the astronomers of his day put in a great deal of effort into explaining the details of the lunar orbit.
They had allowed for the quadripole gravitational moment of Earth due to its oblateness and the effect of the Sun's gravitation but it didn't match until the inc;used the effect of Jupiter's gravitation.
In the end it was a great triumph of Newton's Laws and finally, most astronomers accepted their accuracy.

It's so interesting that from "The traditional model of the Moon" even the ancient Greeks and Ptolemy were very close to the modern orbital characteristics of the Moon but seems nothing like the orbit or the moon in tour flat Earth model. Why is that?

So none of what you quote represents "Lunar Theory in the 20th Century" other than the diagram which shows the inclination of the lunar orbit at 5° very close to the modern 5.15°.


Why are you so far out of date with your references?
A great deal has been learned since the time of Isaac Newton and even since Einstein first published his General Theory of Relativity.

[Tom Bishop]

JSS wrote "We have since proven Einstein right beyond a doubt with much better measurements and countless experiments."
But all you say is "Einstein was highly disputed" which does not refute the statement made by LSS in the slightest.
It is true that originally "Einstein was highly disputed" but since 1915 Einstein's General Theory of Relativity has gained almost, but not quite, universal acceptance.

There is now voluminous experimental evidence supporting GRT. for example:

Acceptance != proven. There were points in history where people accepted the existence of witches too. The three proofs Einstein gave for GR were pretty disputed, and still are criticized by physicists if you care to look.

That illustration might be but the current lunar orbit is no longer described in terms of an epicycle and different (with possibly an equant) but as an approximate precessing ellipse.

Epicycles are still used under the name of Fourier series, which is discussed in the previous quote I gave.

But all you include in your quote is "V. The traditional model of the Moon" and ignore the rest:
"VI. Newton’s Work in Lunar Theory",
"VII. Lunar Theory in the Age of Enlightenment",
"VIII. The Systematic Development of Lunar Theory",
"IX. The Canonical Formalism",
"X. Expansion around a Periodic Orbit" and most importantly
"XI. Lunar Theory in the 20th Century".

And soon after Newton published his "Laws of Motion and Universal Gravitation" Newton and the astronomers of his day put in a great deal of effort into explaining the details of the lunar orbit.
They had allowed for the quadripole gravitational moment of Earth due to its oblateness and the effect of the Sun's gravitation but it didn't match until the inc;used the effect of Jupiter's gravitation.
In the end it was a great triumph of Newton's Laws and finally, most astronomers accepted their accuracy.

As mentioned earlier, the end of that paper says that Newton's laws are not a sufficient explanation:

The three-body problem teaches us a sobering lesson about our ability to comprehend the outside world in terms of a few basic mathematical relations. Many physicists, maybe early in their careers, had hopes of coordinating their field of interest, if not all of physics, into some overall rational scheme. The more complicated situations could then be reduced to some simpler models in which all phenomena would find their explanation. This ideal goal of the scientific enterprise has been promoted by many distinguished scientists [see Weinberg’s (1992) Dream of a Final Theory, with a chapter ‘‘Two Cheers for Reductionism’’]

~

Many physicists may be tempted to see in Newton’s equations of motion and his universal gravitation a sufficient explanation for the three-body problem, with the details to be worked out by the technicians. But even a close look at the differential equations (29) and (30) does not prepare us for the idiosyncracies of the lunar motion, nor does it help us to understand the orbits of asteroids in the combined gravitational field of the Sun and Jupiter.

The "three-body problem teaches us a sobering lesson"... "Many physicists may be tempted to see in Newton’s equations of motion and his universal gravitation a sufficient explanation"... An admission that it can't really explain the situation.

[GreatATuin]

The "three-body problem teaches us a sobering lesson"... "Many physicists may be tempted to see in Newton’s equations of motion and his universal gravitation a sufficient explanation"... An admission that it can't really explain the situation.

Absolutely not. It's the same mistake you make over and over, but I admire your perseverance. That's the "perfect solution fallacy": because there are limitations and difficulties, you seem to assume it doesn't work at all. It would be like saying that because we'll never know the exact numerical value of pi, we really don't have any idea of its value and it could as well be 2 or 5. Just because we don't know everything doesn't mean we don't know anything.

No serious physicist ever said N-body simulators can't be made, because they do exist and they do work very well.

[Tom Bishop]

The "three-body problem teaches us a sobering lesson"... "Many physicists may be tempted to see in Newton’s equations of motion and his universal gravitation a sufficient explanation"... An admission that it can't really explain the situation.

Absolutely not. It's the same mistake you make over and over, but I admire your perseverance. That's the "perfect solution fallacy": because there are limitations and difficulties, you seem to assume it doesn't work at all. It would be like saying that because we'll never know the exact numerical value of pi, we really don't have any idea of its value and it could as well be 2 or 5. Just because we don't know everything doesn't mean we don't know anything.

The author doesn't say it comes close either. He gave up on it and says that physicists may be tempted to see that Newton's laws provide a sufficient explanation, but that is not the case. He says that Newton's laws do not provide a sufficient explanation.

You are only speculating that the attempts come close, claiming that "he got close enough" or whatever, when this is not what is said at all.

No serious physicist ever said N-body simulators can't be made, because they do exist and they do work very well.

They say that the N-body orbits require symmetrical systems. Here is physicist David Gozzard:



 “ Three hundred and fifty years ago Isaac Newton formulated his theory of gravity Newton's theory unified the heavens and the earth under the same physical laws and neatly explained the orbits of the planets, the motion of comets, and how the moon causes the tides. Although Einstein's general relativity has supplanted Newton's theory as a better model of gravity, Newtonian mechanics got us to the moon and are still used to calculate the trajectories of spacecraft throughout the solar system. In spite of this success and more than three centuries of progress we still do not have a neat set of equations that allow us to calculate the orbital parameters of more than two objects at once. This is called the three-body problem, or more generally the n-body problem. ”

"this is a problem because there are certainly more than two bodies in the solar system. We can get around this by formulating equations that give an approximate solution for motions of three or more objects and since the mid twentieth century we've been able to use computers to simulate the orbits using brute force step by step calculations"

So no, they admit that it's not possible and that they need to use approximations and 'brute force' the orbits.

Author goes on to discuss the discovered orbits:



"any slight perturbation to one of the objects will result in chaos with the body either crashing into its orbital partners or being ejected from the group entirely"

And when going over further discovered symmetrical orbits:

"While physically possible, each of these orbits is more unlikely to exist than the last"

That's the state of Newtonian astronomy.

There are some special things they can do to make it look like a Moon going around a planet around a sun, but those don't work out either. They use the Restricted Three Body Problem, where one of the bodies is of zero mass. Even then, the 'Moon' is still chaotic. The benefit of the Restricted Three Body Problem and the Mass-less moon meant that that the moon would be no longer ejected from the system, as it would usually be. It is confined to what is known as "Hill's Region".

From Scholarpedia: http://www.scholarpedia.org/article/Three_body_problem by Dr. Alain Chenciner



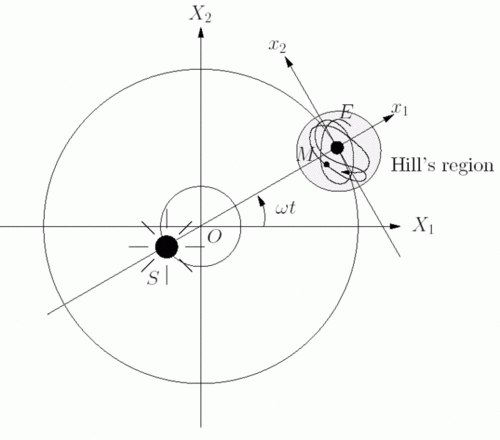
The above depicts a crazy and chaotic moon which even makes a u-turn in mid orbit.

From the text that accompanies the image:

  “ The simplest case: It occurs when, the Jacobi constant being negative and big enough, the zero mass body (we shall still call it the Moon) moves in a component of the Hill region which is a disc around one of the massive bodies (the Earth). This fact already implies Hill's rigorous stability result: for all times such a Moon would not be able to escape from this disc. Nevertheless this does not prevent collisions with the Earth. ”

"Zero mass body" -- One of the bodies in the restricted three body problem is of zero mass.

"Nevertheless this does not prevent collisions with the earth" -- It's still chaotic, even in that simplified version.

Even in this weird version with a mass-less Moon, it doesn't really work.

From Computing the long term evolution of the solar system with geometric numerical integrators by Shaula Fiorelli Vilmart and Gilles Vilmart we see a three body simulation of the Sun-Earth-Moon system created by mathematicians which does use the actual supposed masses of the Earth, Moon and Sun.

Abstract: “ Simulating the dynamics of the Sun–Earth–Moon system with a standard algorithm yields a dramatically wrong solution, predicting that the Moon is ejected from its orbit. In contrast, a well chosen algorithm with the same initial data yields the correct behavior. We explain the main ideas of how the evolution of the solar system can be computed over long times by taking advantage of so-called geometric numerical methods. Short sample codes are provided for the Sun–Earth–Moon system. ”

Sure enough, with the standard algorithm, it fell apart:



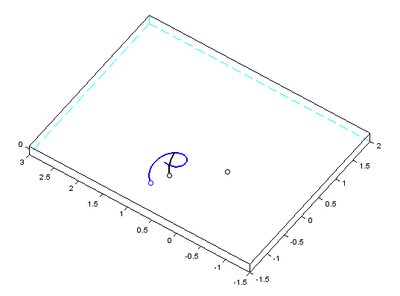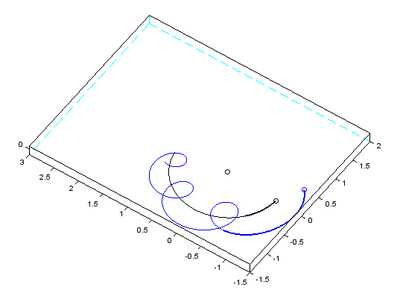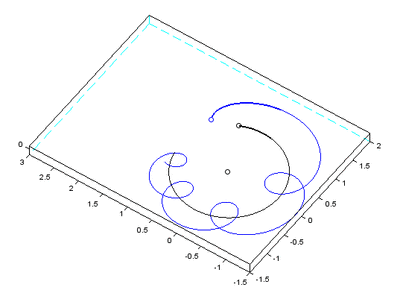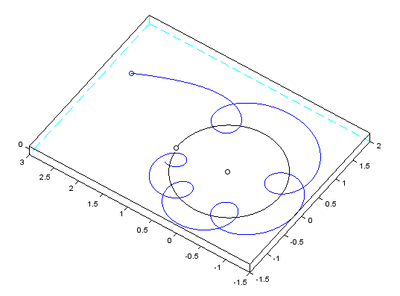
The paper explains that sympectic integrators are necessary and shows a simulation with a working Moon along side this one.

Symplectic integrators are used in particle physics as well (which also has trouble with stability). This abstract of a particle physics paper says:

  “ It has been long understood that long time single particle tracking requires symplectic integrators to keep the simulations stable ”

So again, we see that cheats are necessary.

[GreatATuin]

Well, it's still the same fallacy. You take a video of a guy who says it DOES work with computer simulations even though we don't have what he calls "a neat set of equations" (ie, a formal closed-form solution), he literally says "we can get around this". From that video, you infer that he admits it does not work. If you did that on Wikipedia, you would eventually get banned for backing your statements with citations that say exactly the opposite.

"It's an approximation" still isn't an equivalent of "it doesn't work". Perfect solution fallacy, once again.