How do they predict the Solar Eclipse? Lets go to
their Solar Eclipse website:
1.4 Saros
The Saros arises from a harmonic between three of the Moon's orbital cycles. All three periods are subject to slow variations over long time scales, but their current values (2000 CE) are:
Synodic Month (New Moon to New Moon) = 29.530589 days = 29d 12h 44m 03s
Anomalistic Month (perigee to perigee) = 27.554550 days = 27d 13h 18m 33s
Draconic Month (node to node) = 27.212221 days = 27d 05h 05m 36s
One Saros is equal to 223 synodic months, however, 239 anomalistic months and 242 draconic months are also equal (within a few hours) to this same period:
223 Synodic Months = 6585.3223 days = 6585d 07h 43m
239 Anomalistic Months = 6585.5375 days = 6585d 12h 54m
242 Draconic Months = 6585.3575 days = 6585d 08h 35m
With a period of approximately 6,585.32 days (~18 years 11 days 8 hours), the Saros is valuable tool in investigating the periodicity and recurrence of eclipses. It was first known to the Chaldeans as an interval when lunar eclipses repeat, but the Saros is applicable to solar eclipses as well.
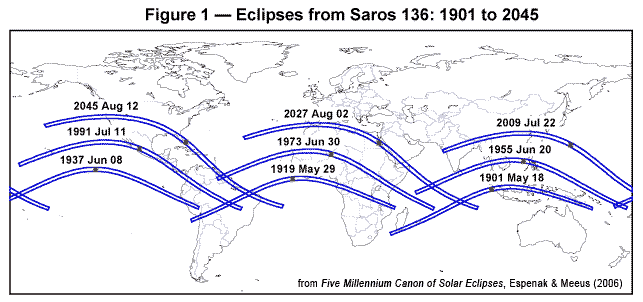
Figure 1 Eclipses from Saros 136: 1901 to 2045
(click for larger figure)
Any two eclipses separated by one Saros cycle share similar characteristics. They occur at the same node with the Moon at nearly the same distance from Earth and at the same time of year. Because the Saros period is not equal to a whole number of days, its biggest drawback as an eclipse predictor is that subsequent eclipses are visible from different parts of the globe. The extra 1/3 day displacement means that Earth must rotate an additional ~8 hours or ~120° with each cycle. For solar eclipses, this results in a shift of each succeeding eclipse path by ~120° west. Thus, a Saros series returns to approximately the same geographic region every three Saros periods (~54 years and 34 days). This triple Saros cycle is known as the Exeligmos. Figure 1 shows the path of totality for nine eclipses belonging to Saros 136. This series is of particular interest because it is currently producing the longest total eclipses of the 20th and 21st centuries. The westward migration of each eclipse path from 1901 through 2045 illustrates the consequences of the extra 1/3 day in the Saros period. The northward shift of each path is due to the progressive increase in gamma from -0.3626 (in 1901) to 0.2116 (in 2045). The color figure Recent Eclipses of Saros 136 shows nine eclipse paths from the series (1937 through 2081).
Saros series do not last indefinitely because the synodic, draconic, and anomalistic months are not perfectly commensurate with one another. In particular, the Moon's node shifts eastward by about 0.48° with each eclipse in a series. The following narrative describes the life cycle of a typical Saros series at the Moon's descending node. The series begins when the New Moon occurs ~17° east of the node. The Moon's umbral/antumbral shadow passes about 3500 km south of Earth and a small partial eclipse will be visible from high southern latitudes. One Saros period later, the umbra/antumbra passes ~250 km closer to Earth's geocenter (gamma increases) and a partial eclipse of slightly larger magnitude will result. After about 10 Saros cycles (~200 years), the first umbral/antumbral eclipse occurs near the South Pole of Earth. Over the course of the next 7 to 10 centuries, a central eclipse occurs every 18.031 years (= Saros), but will be displaced northward by about 250 km with respect to Earth's center. Halfway through this period, eclipses of long duration occur near the equator (mid-series eclipses may be of short duration if hybrid or nearly so). The last central eclipse of the series takes place at high northern latitudes. Approximately 10 more eclipses will be partial with successively smaller magnitudes. Finally, the Saros series ends 12 to 15 centuries after it began at the opposite pole.
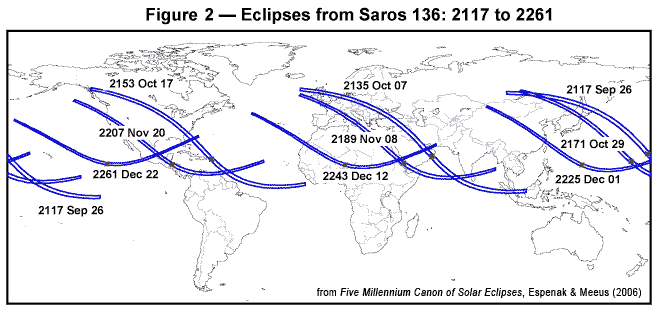
Figure 2 Eclipses from Saros 136: 2117 to 2261
(click for larger figure)
Based on the above description, the path of each umbral/antumbral eclipse should shift uniformly north in latitude after every Saros period. As Fig. 2 shows, this is not always the case. Nine members from Saros 136 are plotted for the years 2117 through 2261. Although the paths of previous eclipses in this series were shifting progressively northward (Figure 1), the trend here is reversed and the paths shift south. This temporary effect is due to the tilt of Earth's axis combined with the passage of Saros 136 eclipses from the Northern Hemisphere's autumnal equinox through winter solstice. Note that the season for this group of eclipses runs from September through December. With each successive eclipse, Earth's Northern Hemisphere tips further and further away from the Sun. This motion shifts geographic features and circles of latitude northward with respect to the Sun-Earth line at a rate that is faster than the change in gamma. Consequently, the eclipse paths appear to shift south in latitude until the winter solstice when they again resume a northward trend.
The scenario for a Saros series at the ascending node is similar except that gamma decreases as each successive eclipse shifts south of the previous one. The southern latitude trend in eclipse paths reverses to the north near the Northern Hemisphere summer solstice.
Because of the ellipticity of the orbits of Earth and the Moon, the exact duration and number of eclipses in a complete Saros series is not constant. A series may last 1,226 to 1,551 years and is composed of 69 to 87 eclipses, of which 39 to 59 are umbral/antumbral (i.e., annular, total, or hybrid). At present (2008), there are 39 active Saros series numbered 117 to 155. The number of eclipses in each of these series ranges from 70 to 82, however, the majority of the series (84.6%) are composed of 70 to 73 eclipses.
Historically speaking, the word Saros derives from the Babylonian term "sar" which is an interval of 3600 years. It was never used as an eclipse period until English astronomer Edmund Halley adopted it in 1691. According to R. H. van Gent, Halley "...extracted it from the lexicon of the 11th-century Byzantine scholar Suidas who in turn erroneously linked it to an (unnamed) 223-month Babylonian eclipse period mentioned by Pliny the Elder (Naturalis Historia II.10[56])."
The page talks egregiously about the Saros Cycle, which is the ancient method of predicting the eclipses.
The Solar Eclipse appears as a little line on the earth, since it is only seen on a narrow path between the sun and moon, and not to everyone. There is also a dynamic component. It moves over time, and can be computed based on the Saros Cycle: "Based on the above description, the path of each umbral/antumbral eclipse should shift uniformly north in latitude after every Saros period." Comments are made of 'because of the tilt of the earth', but the Flat Earth model has an analogue to that as well. We can see that the entirety of this is based on pattern of occurrences, movement, etc. It is not a dynamic Sun-Earth-Moon Round Earth system.
The ancients may not have had enough data to predict world-wide occurrences, but as Rowbotham says, "modern astronomers" have merely improved on the ancient pattern-finding methods.
Surely, if there were a modern way of predicting the eclipse through the computation of a heliocentric or round earth system, it would be used. The fact that we are reading about the ancient flat earth Saros Cycle on
NASA's own website, speaks volumes. It vindicates Rowbotham and entirely discredits modern astronomy.