It took it's time, to follow these argument, but in the end - for me - it appears quite simple.
You know this diagram from http://www.sacred-texts.com/earth/za/za32.htm ?
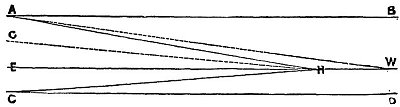
The distance of the vanishing point - aka the horizon - is defined by the limited resolution of the naked eye, where lines from the observers eye E to the vanishing point H and the surface C to H build an angle less than 1 minute of degree.
Rising observers position will broaden this angle and move point H (horizon) farther away, until the 1 minute criteria is met again.
But what, if observer has "hypervision" and could resolve angles less than 1 minute. Is then the point H also moved farther away?
Anyone can get "hypervision": use a binocular or a telescope.
If e.g. the binocular has a magnification of 7x (standard marine binocular) according to this the horizon should be 7 times farther away.
I frequently use such a binocular at sea, but the horizon always appears to be at the same distance, no significant difference when looking with naked eye or with the binocular - unless details get clearer.
Yes, the average human eye resolution is roughly one arc minute (0.0167 degrees).
If we look at the Sun during Lahaina Noon in Hawaii, the angular diameter of the Sun and the distance from the eye gives us the Sun diameter:
2 * 5005 * TAN(0.53/2) = 46.3 km
For 46.3 km to reach vanishing point (if Sun wasn't bright) we would need distance of (46.3 / 2) / tan(0.0167 / 2) = 158 850 km
(But Sun is bright, and we would see its light long beyond vanishing point.)
And yet, Sun "vanishes" at the horizon distance of some 10 000 km.
Even if we make it 20 000, it is still much closer than 158 850 km.
Not only that.
Upper half of Sun is 23.15 km high. Vanishing point at (23.15 / 2) / tan(0.0167 / 2) = 79 425 km.
Lower half of Sun is 23.15 km high. Vanishing point at (23.15 / 2) / tan(0.0167 / 2) = 79 425 km.
Still, lower half, at the same distance as upper half vanishes at those 10 000 km, while upper half takes more time
In cases where the water is turbulent, the shinking ship effect cannot be restored, showing waves to be the cause.
In case where the water is turbulent, the whole surface of the water is turbulent.
Except for rare tsunamis, the reason for water to be turbulent is wind.
There are many accounts in the Flat Earth literature of telescopes restoring half sunken ships across calm bodies of water, showing that they are not really behind a "hill of water".
Such cases are not disputable there (in Flat Earth literature), but here (in reality).
Interesting how this good zoom expanded the ship horizontally all the way to wider than the whole view, and still couldn't bring back the part behind the horizon:
Waves?
What could conveniently stop them from spreading towards us to see them?
Mechanical characteristics of the water surface remains the same all the way.