1

Flat Earth Investigations / Re: Physicist Brian Cox on Universal Acceleration

« on: May 15, 2025, 02:14:05 PM »

Your response perfectly illustrates the deflection tactic I predicted at the outset of this thread.

Less of a deflection tactic and more of a Matthew 7:3-5 take on things.  As to the rest of your post, I've freely admitted here that GR is not something I'm well versed in.  Others here are much more qualified and are doing quite fine at addressing it.

2

Flat Earth Investigations / Re: Physicist Brian Cox on Universal Acceleration

« on: May 14, 2025, 05:51:50 PM »

The flat Earth model accepts the observed upward acceleration without invoking unseen dimensions or speculative theories like space-time curvature. The incredulity lies in the need for such convoluted frameworks when the phenomena can be explained more intuitively.

What non-speculative theory explains how upward acceleration stops the second one steps off the earth until such a time that an object has acquired enough distance from the earth to cause it to accelerate upward at the same rate?

And, while you're at it, please explain what non-speculative theory explains the force causing this upward acceleration.

Then you can tell us what non-speculative theory explains why sunlight travels different distances across the surface of the flat earth.

I guess I already mentioned above that wonderful non-speculative theory that is EA.

3

Flat Earth Investigations / Re: Physicist Brian Cox on Universal Acceleration

« on: May 13, 2025, 08:27:46 PM »

Inventing bizarre physics to fit a Round Earth paradigm is the wrong approach.

This statement from someone who postulates Electromagnetic Acceleration and even has a mathematical, as yet, undefined constant named for him is beyond comical.

4

Philosophy, Religion & Society / Re: Terrible Political Memes

« on: April 29, 2025, 02:21:15 PM »

Seems appropriate this morning.

5

Philosophy, Religion & Society / Re: Trump

« on: April 28, 2025, 03:50:49 PM »

....which should concern you. It doesn't because it's not affecting you.
Yet...

Excellent description of MAGA in a brief statement.  Watching all the MAGA buyer's remorse happening would be comical if what was going on was only affecting them, but it's affecting everyone.

Folks like A80 will go on about people "crying here for criminal migrants" because he doesn't give a shit about anyone but himself right up until ICE breaks down his door without a warrant.

https://newrepublic.com/post/194442/trump-doj-memo-ice-arrest-search-warrant

6

Philosophy, Religion & Society / Re: Trump

« on: April 25, 2025, 07:03:08 PM »

Pretty good explanation of Tom, A80 and the rest of Cult47

7

Science & Alternative Science / Re: Blue Ghost

« on: April 14, 2025, 06:38:46 PM »

And now Katy Perry is "in on it"

Along with those folks from FRAM2.  But then Elon is obviously in on the grift.

8

Philosophy, Religion & Society / Re: Trump

« on: April 09, 2025, 04:56:56 PM »

Congress delegated that power to the executive branch long ago.  Now they have a bill to undo that a bit.

My understanding is Cheeto is using a law granting the President powers to circumvent Congress by declaring a national state of emergency which I believe he did declaring an economic state of emergency which, of course, doesn't exist.  The legislature has the ability to vote to terminate that declaration which is what is being brought to Congress to vote on.  Problem is, the disphits of this country gave republicans, specifically  MAGA morons like MTG, the majority in both chambers so it's not a simple act to get such a resolution passed.

9

Philosophy, Religion & Society / Re: Flat Earth Popularity stronger than ever!

« on: April 03, 2025, 03:14:27 PM »

.... this place remains niche at best.

Perhaps.  But you must remember....

I hope you understand we're maintaining a valuable resource here....

10

Flat Earth Investigations / Re: Solar Eclipse of Aug 12, 2026

« on: February 24, 2025, 04:38:06 PM »

Now, crucially, none of this is at odds with RET. WTF_Seriously just has a very poor understanding of RET, as one would expect.

I have this recent recollection of you saying something to the effect of, "if you have nothing to say...."

And, even then, this requires him to be selective with his eclipses.

Pick a date.

11

Flat Earth Investigations / Re: Solar Eclipse of Aug 12, 2026

« on: February 24, 2025, 04:32:45 PM »

Nice lying. You have selective and partial eclipse paths. This doesn't work on all of them. Here are different views of the August 2027 eclipse:

https://www.timeanddate.com/eclipse/globe/2027-august-2

As Pete said. Aug 2027:



Partial eclipse paths are only a result of the limitations of rotating the model.

12

Flat Earth Investigations / Re: Solar Eclipse of Aug 12, 2026

« on: February 19, 2025, 04:25:47 PM »

At least you're consistent, Pete.  I've got nothing to add.  On the off chance you'd like to join the rest of us and discuss the topic at hand, eclipses, their paths and whether they're plausible on a round earth by all means feel free.  I'd probably be compelled to comment.

13

Flat Earth Investigations / Re: Solar Eclipse of Aug 12, 2026

« on: February 18, 2025, 10:20:58 PM »

I dunno. Why would they? Why would they post maps identical to the one you described as non-representative nonsense? Have you considered telling them that they're misrepresenting RE, and that they should instead selectively glance at timeanddate.com? Considering how trivial it is, as you clearly demonstrated, they'll probably be quite embarassed!

Though... there is an alternative here... hrmmm... Nay, surely that's not it!

Wait.  Wait.  Ohhhhh.  That's a tough one.  Maybe.  A flat projection of the globe is the typical way to show the entirety of the earth in one view even though it's greatly distorted and doesn't accurately represent what is really happening?  Nay, surely that's not it.

https://science.nasa.gov/eclipses/geometry/#:~:text=A%20solar%20eclipse%20occurs%20when,see%20the%20Sun%20completely%20blocked.

Respectfully, you couldn't missed the point any harder if you tried. Hopefully the above helps, but, just in case: the position you're currently trying to defend is not that the Earth is round; it's that the eclipse map presented here is nonsense that doesn't represent RE accurately.

No.  I got the point just fine.  Gotcha!!!!  NASA does the same thing.  WTF So stoOOOpid.  It's your MO.  You won't debate the content of my post because you can't so you resort to deflect and degrade the poster.  You know very well that the NASA animation isn't representative of what actually happens in the round earth model and you know why they create an animation in that way and that it would never be used in an actual debate of eclipse paths between NASA and the FE community.  And no, the point I'm trying to defend is not that the eclipse map is nonsense, that's what you've tried to to turn it into beacuse you have nothing else.

14

Flat Earth Investigations / Re: Solar Eclipse of Aug 12, 2026

« on: February 18, 2025, 03:26:48 PM »

I dunno, man, why would NASA lie about it when WTF_Seriously can crack the code by looking at timeanddate.com for 5 minutes?

https://svs.gsfc.nasa.gov/5236/

Surprisingly poor effort from you, Pete.  You're better than this.

I dunno, why would NASA lie?

https://science.nasa.gov/eclipses/geometry/#:~:text=A%20solar%20eclipse%20occurs%20when,see%20the%20Sun%20completely%20blocked.

"The code" to solar eclipses was cracked long ago, by thousands of people far more intelligent than me but evidently not more intelligent than you since they're all wrong.

Then again, actually looking at timeanddate.com also yields funny results...

I'm sure everyone would like to see you elaborate on this.  I won't hold my breath.

15

Flat Earth Investigations / Re: Solar Eclipse of Aug 12, 2026

« on: February 17, 2025, 08:12:53 PM »

I really wish this website wasn't so entertaining.  It seems everyone is making this harder than it is.

First off, this:

It is of interest that on the globe the paths of the Solar Eclipse look rather odd:

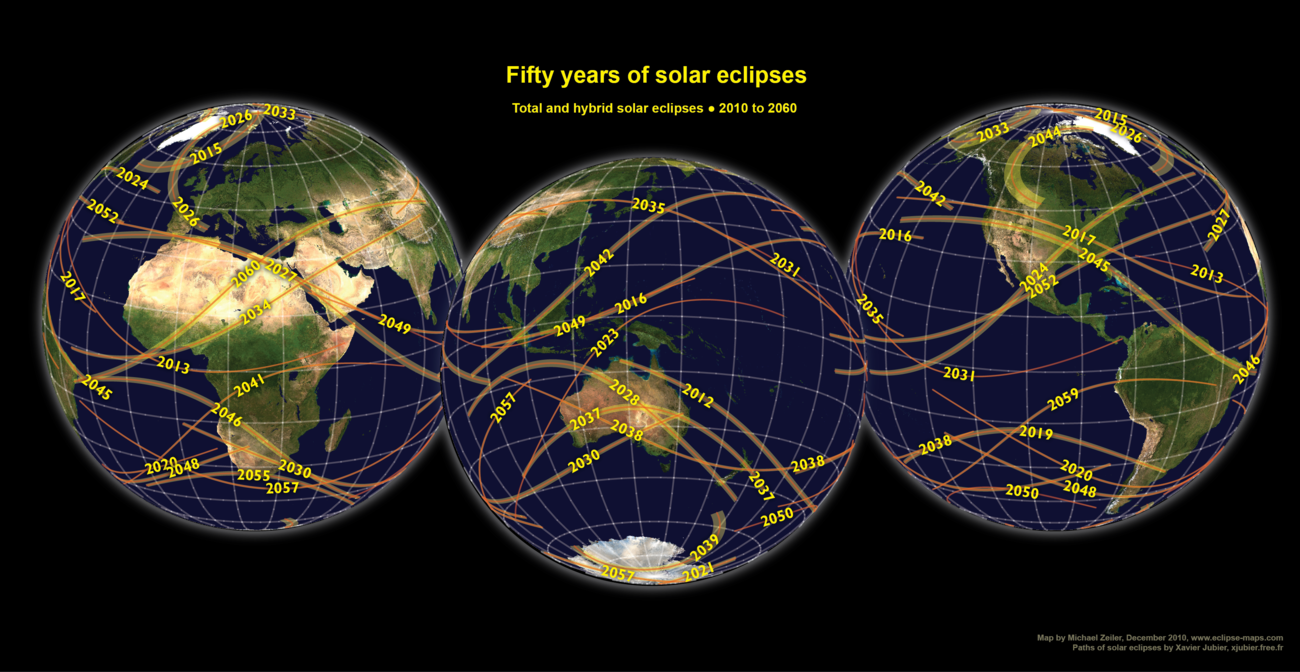
is nonsense.  If, Tom, you’re going to argue, “Gee, RE is silly.” you should use a reference that actually represents RE.  The map is a flat projection and has zero accurate representation of the reality that is the spheroid earth.

The mechanics of every eclipse are exactly the same.  The moon, at 238,000 miles away, crosses in front of the sun in a path across the entire diameter of the earth casting its shadow in various locations due to, well, geometry.  That’s it.  An eclipse path is that of the shadow cast, not the path of the actual moon.  As such, the path can travel differently in the same way  a 50ft. tree can cast a 75 ft. shadow.

Everyone here has been analyzing the situation using 2D maps with the north pole directly at the top.   That’s not reality.  Reality is a 3D object with the north pole tilting toward or away from the direct path of the sun.

The TimandDate website presents a rotatable 3D model of every eclipse.  Play with it a little and put the north pole in a realistic position and you get this:

Every eclipse path is a nearly (not exactly due to the tilted, rotating spheroid shape of the actual earth) straight line all running a horizontal path if the north pole is positioned such that it aligns properly with the inclined orbit of the moon.  It’s almost as if, and bear with me ‘cause this is crazy talk, the shadows are all being caused by an object moving at a consistent angle to N-S in a straight line between a spheroid and a distant light source.

16

Flat Earth Theory / Re: Finding Polaris and FE model

« on: August 16, 2024, 06:49:07 PM »

The Sun moves North and South in addition to East and West. It's easier to get a coordinate by a static celestial object rather than a variable one. The Latitude in the North is thus based on Polaris.

For example, how would they determine 90 degrees North at the Geographic North Pole? By the North Star, right? How about 85 degrees North? How about 5 degrees North? Obviously, the North Star is used for this coordinate and not the Sun.

So what's the coordinate reference for latitude in the south?

17

Flat Earth Theory / Re: New idea on observing Sigma Octantis from multiple locations

« on: April 16, 2024, 10:10:32 PM »

There might be a time when two of the three southern continent locations such as South America and Africa see the night stars at the same time, but never all three (South America, Africa and Australia) at the same time.

https://www.timeanddate.com/worldclock/sunearth.html

Here is summer on June 21, 2021 with added green marker for "a star":

Nice cherry picking of data.  You've been shown before that this isn't true.

From the same website:



Now locate the star between the southern tip of Aftica and Madagascar on your monopole map and all three continents can view it at the same time except that South America and Australia will be looking nowhere near south as happens in reality.

18

Flat Earth Theory / Re: New idea on observing Sigma Octantis from multiple locations

« on: April 15, 2024, 06:37:37 PM »

Both of Tom's videos are nonsense.

First, if all of the celestial bodies are inside the dome then shining lights on the dome from outside is meaningless.  That's neither here nor there though to their problems.

The first video is simply magician's sleight of hand and optics.  What we want to see is not what the top of the dome looks like but what the map looks like.  The video never shows this.  To see what is really going on the camera should be either able to view the map underneath or be viewing the bottom of the glass.  Optically, the shadow on the exterior of the dome is due to the fact that the light angle is causing all of the light to be reflected back in.  It's how a fiber optic cable works.  At the proper angle, light is reflected back into the core off the cladding as it propagates down the fiber.  All we are seeing is this optical property of the light angle causing all the light to be reflected back into the dome which causes the outer shell of the dome to be dark. You can see this by being able to slightly view the map and times when the magician is causing a shadow as well as you can see a bright outline on the paper, opposite the light, where the light would be shining at a nearly 90 degree angle to the edge of the dome and passing out.

In the second video, the lights should be directly above the camera circling like a clock not off to the side to match the FE model.

Neither video is in any way an valid representation of what is happening on a flat earth.

19

Flat Earth Investigations / Re: I am wondering why I do not see...

« on: April 11, 2024, 10:16:32 PM »

Why is the Moon's shadow at the time of the Total Solar Eclipse placed elsewhere other than the plane of the ecliptic upon the earth? The time of the Total Eclipse should be where the Moon intersects the Sun on the Ecliptic.

The simple and obvious answer to this is because the earth's not flat with the sun and moon circling above it around a central point.  You've asked the exact question that proves the FE model false.

During a solar eclipse, the declination of the moon and sun are identical.  In the FE world that puts two objects of nearly equal size directly on top of each other over the exact same latitude line.  IF FE were true, at the time of the total eclipse totality must occur at a latitude equal the declination of both.  Having the time of the eclipse occur toward the polar latitudes is geometrically impossible.

It is the fact that you have objects orbiting and rotating on different planes that gives you the answer to your question.

20

Arts & Entertainment / Re: Official Sports Thread

« on: January 17, 2023, 03:45:26 PM »

The problem with (arguably) being the GOAT is that being just above middle is taken as an embarrassment.  Brady's still above 19 other league QBs on Garygreens chart and TB as a team is right in the middle on the other.

Mayfield or Wentz would give their left nut to be as shitty as Brady.