[rabinoz]

The Earth does technically "move away" from the observer exponentially... if it is round. The "curve" isn't linear, as in, a flat slope.

If you square the whole equation you provided you end up with something very similar to the 8" of curvature per distance squared formula you've undoubtedly seen used numerous times here.

On a flat earth, viewing distance is a lot simpler, using only a triangle and Pythagoras theorem you can calculate how far per height rather easily. This would be a good way to test both theories if some interested parties would like to partake in an experiment to test these variables.

And don't forget, the magical wild card we call refraction.

https://en.wikipedia.org/wiki/Horizon#Effect_of_atmospheric_refraction

What's more interesting to me is the section immediately following the one above.

Curvature of the horizon
This section has multiple issues. Please help improve it or discuss these issues on the talk page.
This section does not cite any sources. (June 2013)
This article's factual accuracy is disputed. (June 2013)
This section requires expansion with: examples and additional citations. (June 2013)

Seems even Wikipedia takes issue with facts being presented without sources, even one something as mundane as the curvature of the earth in relation to the horizon.

Then the vanishing point section directly beneath that has some interesting information. Indicating that the horizon is treated as any other plane, without curvature being a factor in regards to perspective whatsoever.
[/quote]
Firstly, I am afraid you are completely mistaken with "The Earth does technically "move away" from the observer exponentially... if it is round." NO it DOES not! Do you know what "exponentially means"? Obviously not. It means a variation with some constant, commonly e. So an exponential variation would have:
distance = (some constant) x e^{(height/constant)}.
Study up on your math a bit!

Elevation	Horz dist d = 3.57xh0.5	Horz (Exp)
0 m	0.0 km	0.7 km
2 m	5.0 km	5.0 km
5 m	8.0 km	101.4 km
7 m	9.4 km	749.3 km
10 m	11.3 km	15050.1 km

An exponential variation and a square root variation are completely different animals (or whatever - they are as different as chalk and cheese!)

Of course the equation I gave essentially agreed with the 8"/(mile squared) - I never claimed any differently! I'm not getting into "curvature of the horizon" apart from: The horizon looks flat from even quite high altitudes - the earth is huge! What can be measured is the dip from horizontal to the horizon at increasing altitude. It is small and not apparent to the naked eye - about 0.5° from 300 m or 0.9° from 1,000 m. A surveyor can measure this quite readily (of course they are part of the conspiracy ). On "vanishing point", it is only a drawing aid! The horizon is not any "magic" vanishing point. The ultimate vanishing point is an indefinite distance away. Of course in drawing we (not me - can't draw for nuts!) draw the horizon as FLAT, it looks FLAT! Imagine sitting it a boat on a perfectly smooth lake. On a Globe of Flat Earth the horizon would be exactly the same all around us - flat. I would contend that (on a clear day) the horizon: on the Globe would be sharp (and close), while on the Flat Earth it would be quite indistinct and an indefinite distance away. Look at the picture at the right (from a Flat Earth Video I might add), taken at quite high zoom. Quite apart from any other issues, clearly the horizon is not the vanishing point! The buildings are certainly further away than the horizon, yet show quite clearly.

From Horizon Zoom Boom Earth Flat

I hope there are not too many glaring mistakes because:

As it is written:
When you've gotta go, you've gotta go!

[Orbisect-64]

All I'm saying is that you can express yourself with a lot less verbiage and still be concise.

So far I see a lot of filler designed to look like a coherent, original thought.

Explain why perspective is flawed.

Explain why you think atmospheric conditions aren't a reasonable explanation for viewing distance.

Also tell me why you think cognitive dissonance only affects flat earthers and not round earthers.

Not trying to just be rude, but I think it's rude to assume someone has 30 minutes to carefully read a post that should be at least half as long and twice as easy to follow.

And to call me a flat earther is you're attempt at discrediting me, even though nowhere in my post did I even make an inclination of my stance.

LOL! You so NAILED that rabinoz. You would almost think you know Giants Orbiting personally. 

[TheTruthIsOnHere]

Firstly, I am afraid you are completely mistaken with "The Earth does technically "move away" from the observer exponentially... if it is round." NO it DOES not! Do you know what "exponentially means"? Obviously not. It means a variation with some constant, commonly e. So an exponential variation would have:
distance = (some constant) x e^{(height/constant)}.
Study up on your math a bit!

Elevation	Horz dist d = 3.57xh0.5	Horz (Exp)
0 m	0.0 km	0.7 km
2 m	5.0 km	5.0 km
5 m	8.0 km	101.4 km
7 m	9.4 km	749.3 km
10 m	11.3 km	15050.1 km

An exponential variation and a square root variation are completely different animals (or whatever - they are as different as chalk and cheese!)

I'm so glad that Orbisect brought this thread back up. I almost missed how you tried to school me on math and exponential equations and completely blew it.

Now let me help you out rabinoz, I know you haven't been to school in about 40 or 50 years, and maybe things have changed since the 50's.

First the difference between something that is linear and exponential.

A linear equation represents a line that travels along a slope in a straight flat line.
Example of a straight line formula


Example of a straight line plotted on a Cartesian coordinate system:


An exponential function describes a line that travels in an increasingly curved line:

Graphed:


A parametric equation, is one that can describe a curved line, it can be parabola, a circle, or countless other odd lines.
Example of the equation for the circle:

A circle on the same type of graph:


As you can see the equation for a straight line and something else is obviously very different. One has exponents, and one doesn't. In case you don't remember what an exponent is: y^{2<-- this is a exponent}. Different types of lines will have different exponents, it's not always squared. But in our case, a curved line equation deals with squared variables. This is why you can "square" that cute little equation you gave and it will still technically resolve into the "8 inches per mile squared for a 6' tall observer" little ditty you see floating around.

Technically, the horizon on a curved Earth would move away from you exponentially, in the sense that it doesn't move away from you in a linear fashion. Maybe you should study up on your math a bit. Break out that trust abacus you used to use in Senior High.

[rabinoz]

Firstly, I am afraid you are completely mistaken with "The Earth does technically "move away" from the observer exponentially... if it is round." NO it DOES not! Do you know what "exponentially means"? Obviously not. It means a variation with some constant, commonly e. So an exponential variation would have:
distance = (some constant) x e^{(height/constant)}.
Study up on your math a bit!

Elevation	Horz dist d = 3.57xh0.5	Horz (Exp)
0 m	0.0 km	0.7 km
2 m	5.0 km	5.0 km
5 m	8.0 km	101.4 km
7 m	9.4 km	749.3 km
10 m	11.3 km	15050.1 km

An exponential variation and a square root variation are completely different animals (or whatever - they are as different as chalk and cheese!)

I'm so glad that Orbisect brought this thread back up. I almost missed how you tried to school me on math and exponential equations and completely blew it.
Now let me help you out rabinoz, I know you haven't been to school in about 40 or 50 years, and maybe things have changed since the 50's.

You really do have a sense of humour with your "Now let me help you out rabinoz", or more like a blown up sense of you own self-importance.
And yes, I know a "square root variation" can be turned into a quadratic variation by changing the independent variable!

You're a bit out there as it happens, by a few decades, but things like this haven't changed in centuries! A lot of "higher maths" has, but not this elementary stuff!
In any case, after school, it was university, then teaching in electrical engineering. Things like logarithmic and exponential variations are rather vital in that field. In fact much of the work involves complex (as in complex numbers etc, you know the x + iy stuff), plus all the stuff solving higher order polynomials (comes into finding the poles and zeros of linear network transfer functions) and numerical optimisation.

First the difference between something that is linear and exponential.
A linear equation represents a line that travels along a slope in a straight flat line.
Example of a straight line formula

Example of a straight line plotted on a Cartesian coordinate system:

Get on with it! Of course I know the elementary stuff.

An exponential function describes a line that travels in an increasingly curved line:

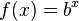
Graphed:

Yes, no problem with that! But the critical thing is that to be an "exponential variation" the exponent must contain the independent variable!
As does your equation f(x) = b^x.
Actually though it's more than an "travels in an increasingly curved line", a cubic equation does that, but an exponential variation "travels in an exponentially increasingly curved line". All the derivatives of the simple exponential function are themselves exponentials. I do hope you know what all this means!

A parametric equation, is one that can describe a curved line, it can be parabola, a circle, or countless other odd lines.
Example of the equation for the circle:

A circle on the same type of graph:

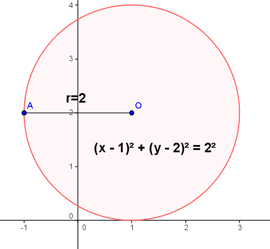
Sure, I guess any equation can be written in parametric form, and most can be written in non-parametric form, but often these have multi-valued solutions as the case for a circle where:
y = (r² - x²)^1/2. For each value of x in the range -r <= x <= +r there are 2 values of y.

As you can see the equation for a straight line and something else is obviously very different. One has exponents, and one doesn't. In case you don't remember what an exponent is: y^{2<-- this is a exponent}. Different types of lines will have different exponents, it's not always squared. But in our case, a curved line equation deals with squared variables. This is why you can "square" that cute little equation you gave and it will still technically resolve into the "8 inches per mile squared for a 6' tall observer" little ditty you see floating around.

Now you are starting to get screwed up. Just because an equation has exponents does not make the variation exponential!
A quadratic equation such as f(x) = ax² + bx + c contains an exponent, but since it is a constant exponent (2) it does not represent an exponential variation.

Technically, the horizon on a curved Earth would move away from you exponentially, in the sense that it doesn't move away from you in a linear fashion.

No, just because a variation is not linear does not make it an exponential variation.
A quadratic variation is not linear but it not an exponential variation either.

So, "technically, the horizon on a curved Earth" definitely does not "move away from you exponentially".
The variation can be approximated by a quadratic variation (like the old 8" x miles² not bad to even hundreds of miles).
This variation contains an exponent, 2, but is not an exponential variation

Maybe you should study up on your math a bit. Break out that trust abacus you used to use in Senior High.

Sure, I could be a little rusty on Laplace transforms, the more difficult trigonometric identities and complicated integration, but trivial stuff like this is child's play.

And, no I never used an abacus, though I gather an expert can do wonders on them. In high school we had to put up with log and trig tables. Then onto slide-rules (which really are a mechanical version of log tables) for multiplication, division and exponentiation and the good old "Mark I brain" for addition and subtraction and graph paper for plotting. When the HP-35 calculator was released everyone thought it was "magic", but I waited till 1973 (I happened to be at UCB and HP that year) and got an early HP-45 and have stuck with them ever since, through the HP-65, HP-41c and finally an HP-48 (which I no longer use). Of course since 1962 with the installation of the old GE-225 computer and later computers repetitive stuff was done of these bigger machines.

Now, strangely enough I do most calculation in Excel on a Windows PC, though an HP-41c emulator on Android phone and tablet is great for quick little sums - has all the nice functions for trig and all that, plus a bit of storage - it does make a nice replacement for you little abacus!

No, I for this stuff I really don't think I need much extra study, but I sure get bogged down on GR and stuff like that! I even struggle a bit with spherical geometry.

But, you most certainly "should study up on your math a bit". Maybe try this - seems about you level: Math Videos for Grade 8 Algebra 1, Exponential and Linear Functions

Even Wikipedia would set you straight: Exponential growth Exponential growth occurs when the growth rate of the value of a mathematical function is proportional to the function's current value, resulting in its growth with time being an exponential function. Exponential decay occurs in the same way when the growth rate is negative. In the case of a discrete domain of definition with equal intervals, it is also called geometric growth or geometric decay, the function values forming a geometric progression. The formula for exponential growth of a variable x at the (positive or negative) growth rate r, as time t goes on in discrete intervals (that is, at integer times 0, 1, 2, 3, ...), is   xt = x0(1+r)t   where x0 is the value of x at time 0. For example, with a growth rate of r = 5% = 0.05, going from any integer value of time to the next integer causes x at the second time to be 5% larger than what it was at the previous time. Since the time variable, which is the input to this function, occurs as the exponent, this is an this is an exponential function. From Wikipedia, the free encyclopedia, Exponential_growth

Spacer

The graph illustrates how exponential growth (green) surpasses both linear (red) and cubic (blue) growth. (red) linear growth (blue) cubic growth (green) exponential growth

Hope I didn't make too many little typos in this!
But it's getting a bit bit late and you know how these poor geriatrics need their sleep, especially after using pick and shovel to fix up the wrecked garden we have!

[TotesNotReptilian]

blah blah blah... 8th grade math... blah...

more 8th grade math... blah...

Yes yes, both of you are very smart.

Do you know what "exponentially means"? Obviously not. It means a variation with some constant, commonly e. So an exponential variation would have:
distance = (some constant) x e^{(height/constant)}.
Study up on your math a bit!

*ahem* TheTruthIsOnHere was correct in stating your original description of an exponential equation was wrong.

A parametric equation, is one that can describe a curved line, it can be parabola, a circle, or countless other odd lines.
Example of the equation for the circle:

*ahem* This description of parametric equations is also wrong. This isn't a parametric equation. Not that it is relevant anyway...

[TheTruthIsOnHere]

blah blah blah... 8th grade math... blah...

more 8th grade math... blah...

Yes yes, both of you are very smart.

Do you know what "exponentially means"? Obviously not. It means a variation with some constant, commonly e. So an exponential variation would have:
distance = (some constant) x e^{(height/constant)}.
Study up on your math a bit!

*ahem* TheTruthIsOnHere was correct in stating your original description of an exponential equation was wrong.

A parametric equation, is one that can describe a curved line, it can be parabola, a circle, or countless other odd lines.
Example of the equation for the circle:

*ahem* This description of parametric equations is also wrong. This isn't a parametric equation. Not that it is relevant anyway...

The funny thing is I really maxed out around this level of math. I actually failed Calculus in 12th grade. Rab obviously went on to learn more insanely complicated mathematic, well beyond my definition of practicality. I don't even know why he decided to talk about "exponential variation," whatever that means. I certainly didn't bring that up. I don't even remember how this conversation devolved into a history lesson on the graphing calculator, and really what any of this math even has to do with the OP.

Point being, the horizon curves away from you on a round earth. On a flat earth I feel you would technically be able to see further with increased altitude, and then as shown in the photos posted in the thread is when the atmosphere would have the most pronounced effect on your visibility. The fact still remains that there are countless photographs on the internet that clearly exhibit being able to see further than you *mathematically* should be able to. And yes, I accept photographs as evidence. Unless it's a photograph mathematically impossible to take, like one of the Earth from a million miles away.

[TotesNotReptilian]

Point being, the horizon curves away from you on a round earth. On a flat earth I feel you would technically be able to see further with increased altitude, and then as shown in the photos posted in the thread is when the atmosphere would have the most pronounced effect on your visibility.

Forgive me if I don't trust your "feeling". Please provide a reason why we would be able to see further. (Hints: 1. Obstacles 2. Atmosphere)

The fact still remains that there are countless photographs on the internet that clearly exhibit being able to see further than you *mathematically* should be able to.

Example? I haven't seen any. Keep in mind, there are a lot of flat earth youtubers out there who don't know the first thing about geometry. You need to check their math and facts carefully. I recommend starting a new thread if you want to post a bunch of photos as evidence.

And yes, I accept photographs as evidence. Unless it's a photograph mathematically impossible to take, like one of the Earth from a million miles away.

Good for you. However, there is nothing mathematically impossible about taking a photo from a long way away. It is only logistically difficult. Very difficult. And yet we managed to do it anyway. Neat!

[rabinoz]

. . . . . . . . . . . . . . . . . . . . . .
Yes yes, both of you are very smart.

Yes, I was "trying to be smart", simply because TheTruthIsOnHere raved on for pages, "showing off how smart he was" claiming I knew nothing of maths. He was completely false in claiming that the variation in distance with elevation was exponential, and it most certainly is not, not even in the "colloquial sense" of "very rapidly".
I guess I came on a bit heavily, but so far I believe I was and am completely correct.

Do you know what "exponentially means"? Obviously not. It means a variation with some constant, commonly e. So an exponential variation would have:
distance = (some constant) x e^{(height/constant)}.
Study up on your math a bit!

*ahem* TheTruthIsOnHere was correct in stating your original description of an exponential equation was wrong.

My post that started this was

Except on a round earth, if the horizon is the curvature itself, going up you shouldn't be able to see as far as you would on a flat earth. The horizon would technically be traveling exponentially away from you.

(and I replied)

[/i]
Yes, most of your first bit is essentially correct, but then you say "The horizon would technically be traveling exponentially away from you."
The distance to the horizon does increase with altitude, but certainly not "exponentially" as you claim. It increases as the square root of distance, much, much different.

^{An approximate expression is:}

Where h is in metres and d is in km.

Where claims " The horizon would technically be traveling exponentially away from you." he is completely incorrect!
[/quote]
Please explain yourself when you say "he is completely incorrect!", because I simply do not agree!

The approximate variation of horizon distance with elevation is not exponential but a square root relationship! as

d = 3.57 x h^1/2, which contains the exponent (1/2), but is definitely NOT an exponential relationship.

The form of exponential variation I gave:

distance = (some constant) x e^{(height/constant)}

.
is quite correct, though the base does not have to be e.

The crux of this whole matter is that an expression, such as x³can contain an exponent, (3 in this case - making this a cubic variation), and NOT be an exponential variation.

To be an exponential variation, the exponent MUST contain the independent variable (x in this case) in some form, such as distance = (some constant) x e^{(height/constant)}, where height is the independent variable.

There is a big difference in the type of variation between something like a square root, as in:

and an exponential variation. The graph below compares the type of variation we get with the above approximation and an exponential variation - purely hypothetical):

Exponential v. Square Root Variation - different "animals"

As you see here the exponential variation climbs at an ever increasing rate, while the square root variation climbs more slowly and at a decreasing rate.

[rabinoz]

The funny thing is I really maxed out around this level of math. I actually failed Calculus in 12th grade. Rab obviously went on to learn more insanely complicated mathematic¹, well beyond my definition of practicality. I don't even know why he decided to talk about "exponential variation," whatever that means. I certainly didn't bring that up. I don't even remember how this conversation devolved into a history lesson on the graphing calculator, and really what any of this math even has to do with the OP.

Well, I brought "exponential" up because this statement in an earlier post of yours:

The horizon would technically be traveling exponentially away from you.

I did obviously interpret "traveling exponentially away from you. as being an exponential variation, so I made what I thought was a reasonable post saying that it was not an exponential variation. You then come back with your pages stuff saying I was wrong and needed to study some maths. Well, I guess I reacted a bit, but all I did was answer each point you made. If you don't have much maths knowledge, that's OK, not everyone does - but in that case be a little careful how you criticise.

Your claim lead me to think you thought you had a fair understanding. I guess we had better forget that whole episode.

Just to finish off, your earlier post also included:

You can see further the higher up you go, until eventually your vision fails or the atmospheric conditions inhibit your viewing distance. This would be true on a flat or a round earth.
. . . . . . . . . . . . . . . . . . . . .
In a plane the horizon appears faded, and not the sharp line you guys are saying it is. Why is that the case?

• The explanation is straight forward on the globe:
  At ground level the horizon is fairly close (a few miles), so (except in "hazy" weather - or in LA!) we see it as a sharp line.
  From an aircraft at 30,000 ft the horizon distance would be around 200 miles, so we are looking through much more of air. Even in perfectly clear air, at ground level, there is a limit to visibility of around this distance due to "Rayleigh scattering". As a result we see a bluish haze above the horizon, getting clearer with altitude as we are seeing through less dense air.
  
• This has to be my opinion because I don't think the earth is flat.
  On the earth were flat I would think that even at ground level we would be already be looking through a large amount of air thickness, so would always see a hazy horizon, and that going to a higher altitude should not make much difference.
  
  You'd better get a FE expert on this!

[1] I guess I had to in "Electrical Engineering" - even then I would have fared better if I more "higher maths"!

[TotesNotReptilian]

Ah, I see what you were getting at now. To be fair to TheTruthIsOnHere, the original part that I quoted was pretty confusingly worded. I have a pretty strong math background, and I still had no idea what you meant.

Anyway, don't mind me. I have a weakness for being snarky. Cheers.

[TheTruthIsOnHere]

On a flat earth it is a matter of using the Pythagorean theorem to calculate viewing distance. The relationship between the observed, the observer, and the angle of viewing is represented very neatly by a triangle. Your vision would become more obscured by atmospheric interference when you go high up. Interestingly enough, however, the horizon does seem to always rise to the eye of the observer regardless of height.

On a round earth it is exponetially *gasp* more complicated. How do you calculate the distance to the horizon for your altitude without a navy manual?

No one can answer me as to why, if the horizon is the tangent of your position and the Earth's curvature, why would the horizon rise to meet your eye. Or, if the horizon is literally the earths curvature, why is the horizon not curved to a similar degree all around you. Is the Earth really a cylinder?

[rabinoz]

On a flat earth it is a matter of using the Pythagorean theorem to calculate viewing distance. The relationship between the observed, the observer, and the angle of viewing is represented very neatly by a triangle.

I will try to tackle the rest later, after you show just how you use "Pythagorean theorem to calculate viewing distance" on the flat earth.
Honestly I have never seen that and cannot see how it could ever be done. So, I am very interested.

[TheTruthIsOnHere]

On a flat earth it is a matter of using the Pythagorean theorem to calculate viewing distance. The relationship between the observed, the observer, and the angle of viewing is represented very neatly by a triangle.

I will try to tackle the rest later, after you show just how you use "Pythagorean theorem to calculate viewing distance" on the flat earth.
Honestly I have never seen that and cannot see how it could ever be done. So, I am very interested.

Sorry, I misapplied Pythagoras, It's actually a trigonometric application, thanks for jostling my brain a little. If you know your altitude, and you know your angle of viewing, then you can solve the bottom leg of the triangle. Assuming the earth is flat, let's represent it as the sea being flat to the horizon, and if we are looking down at an object before the horizon, say tilted POV of 45degrees, and you know your height, you can solve how far away that object is. But as I said, interestingly enough, if you are looking at the horizon, from any altitude your viewing angle will be 90 degrees. So it really is a tricky problem to solve.

Tell me exactly how one calculates the distance to the horizon on a curved earth, without navy manuals. Is it some obscure geodetic equation of curved triangles or what?

[TotesNotReptilian]

Sorry, I misapplied Pythagoras, It's actually a trigonometric application, thanks for jostling my brain a little. If you know your altitude, and you know your angle of viewing, then you can solve the bottom leg of the triangle. Assuming the earth is flat, let's represent it as the sea being flat to the horizon, and if we are looking down at an object before the horizon, say tilted POV of 45degrees, and you know your height, you can solve how far away that object is. But as I said, interestingly enough, if you are looking at the horizon, from any altitude your viewing angle will be 90 degrees. So it really is a tricky problem to solve.

You almost got it. Yes, that will correctly give you the distance an object is away from you. Looking directly at the horizon gives 90 degrees, which correctly gives an infinite distance. But that doesn't really tell us the maximum viewing distance does it? Is the maximum distance really infinite?

Tell me exactly how one calculates the distance to the horizon on a curved earth, without navy manuals. Is it some obscure geodetic equation of curved triangles or what?

The exact equation is this:

d = R cos^-1(R/(R+h))

d = distance to horizon
R = radius of earth
h = height above the earth
* if your calculator uses degrees instead of radians, multiply your answer by pi/180

This equation is very sensitive to rounding errors due to how small h is compared to R. Which is why an approximation is usually used. rabinoz gave this one earlier:

d = 3.57 h^1/2

d is in kilometers, h is in meters. I double-checked, it is correct. This approximation is very accurate when h is much less than R. It is derived using a small angle approximation for the original equation. Nothing obscure about it. I can show you the derivation of either equation if you want.

No one can answer me as to why, if the horizon is the tangent of your position and the Earth's curvature, why would the horizon rise to meet your eye.

I assume by "the horizon rise to meet your eye", you mean that you can look straight ahead to look at the horizon, as opposed to tilting your gaze down a few degrees? Luckily, we don't have to guess how much you need to tilt your head, we can calculate it easily!

tilt downward = d/R
* answer given in radians. to get degrees, multiply by 180/pi.
* feel free to double check this. I derived it on the spot.

Yep, that easy. As you can imagine, this is usually going to be pretty small, considering how big the radius of the earth is. It is detectable on an airplane though, assuming straight and level flight. Try it out next time you are on an airplane!

Edit: Using a cruising altitude of 45,000 feet, the tilt downward to the horizon would be 3.7 degrees. Not super easy to detect, but doable with the right instrument.

Or, if the horizon is literally the earths curvature, why is the horizon not curved to a similar degree all around you. Is the Earth really a cylinder?

I'm not sure what you mean by this. Yes, the horizon curves the same amount in every direction. The equations given will work no matter what direction you are facing. It isn't a cylinder.

Edit: none of the above takes into account refraction, which could be significant over long distances

[Chris C]

Your first picture shows no curve either.  Wouldn't you expect to find that on a round-earth?

No one should expect to see a curve.

[rabinoz]

On a flat earth it is a matter of using the Pythagorean theorem to calculate viewing distance. The relationship between the observed, the observer, and the angle of viewing is represented very neatly by a triangle.

I will try to tackle the rest later, after you show just how you use "Pythagorean theorem to calculate viewing distance" on the flat earth.
Honestly I have never seen that and cannot see how it could ever be done. So, I am very interested.

Sorry, I misapplied Pythagoras, It's actually a trigonometric application, thanks for jostling my brain a little. If you know your altitude, and you know your angle of viewing, then you can solve the bottom leg of the triangle. Assuming the earth is flat, let's represent it as the sea being flat to the horizon, and if we are looking down at an object before the horizon, say tilted POV of 45degrees, and you know your height, you can solve how far away that object is. But as I said, interestingly enough, if you are looking at the horizon, from any altitude your viewing angle will be 90 degrees. So it really is a tricky problem to solve.

Tell me exactly how one calculates the distance to the horizon on a curved earth, without navy manuals. Is it some obscure geodetic equation of curved triangles or what?

As you say if, on a flat earth you are looking down a point on the ground at a know angle you calculate your distance to it. Actually, since the "curvature" of the globe is actually quite small, you can do the same thing for objects on the Globe with little error for distances up to a few kilometres.

Sure, I certainly agree that on a flat earth "if you are looking at the horizon, from any altitude your viewing angle will be 90 degrees. So it really is a tricky problem to solve." This is simply because there is no "real horizon" on the flat earth. Your vision would just fade into a blur, with the distance being limited by the clarity of the air. This could be anywhere from a few kilometres ( in LA?  ) to a few hundred kilometres for extremely clear air (the so-called Rayleigh limit).

Then you ask "Tell me exactly how one calculates the distance to the horizon on a curved earth, without navy manuals. Is it some obscure geodetic equation of curved triangles or what?" - just a bit of Pythagoras + a bit of algebra to simplify it - no "obscure geodetic equation"!

There are lots of references to this on the internet.
How to Calculate the Distance to the Horizon - www.wikihow.com/
How to Calculate the Distance to the Horizon - Boatsafe.com
Distance to the Horizon - www-rohan.sdsu.edu/
I will reproduce a little of the last one. It does go on to include the effects of refraction.

Spacer

Distance to the Horizon It shows a vertical plane through the center of the Earth (at C) and the observer (at O). The radius of the Earth is R, and the observer's eye is a height h above the point S on the surface. (Of course, the height of the eye, and consequently the distance to the horizon, is greatly exaggerated in this diagram.) The observer's astronomical horizon is the dashed line through O, perpendicular to the Earth's radius OC. But the observer's apparent horizon is the dashed line OG, tangent to the surface of the Earth. The point G is the geometric horizon. Elementary geometry tells us that, because the angle between the dashed lines at G is a right angle, the distance OG from the observer (O) to the horizon (G) is related to the radius R and the observer's height h by the Pythagorean Theorem: (R + h)2= R2 + OG2 or OG2 = (R + h)2 − R2 . But if we expand the term (R + h)2 = R2 + 2 R h + h2, the R2 terms cancel, and we find OG = sqrt ( 2 R h + h2 ) . It's customary to use the fact that h << R at this point, so that we can neglect the second term. Then OG ≈ sqrt ( 2 R h ) is the distance to the horizon, neglecting refraction. Numerically, the radius of the Earth varies a little with latitude and direction; but a typical value is 6378 km (about 3963 miles). If h is in meters, that makes the distance to the geometric horizon 3.57 km times the square root of the height of the eye in meters or about 1.23 miles times the square root of the eye height in feet. From: ROHAN Academic Computing at San Diego State University: Distance to the Horizon

Another point that I think is just as important in the Dip Angle to the horizon. This is a measure of how far the horizon on the Globe is below true horizontal and it is a lot smaller that you might imagine. this reference (from the same place) looks at it: Dip of the Horizon - www-rohan.sdsu.edu/.
Here are just a few values:

Height	Spc	Dip angle
0 m	Spc	0.00°
10 m	Spc	0.10°
100 m	Spc	0.32°
1,000 m	Spc	1.02°
10,000 m	Spc	3.20°

These angles (certainly for over 100 m) are easily measurable by a surveyor (Geodetic or not), but not discernable with the unaided eye.

In other words those that say "But the horizon always rises to eye-level" are nearly correct. If you are 100 m above sea-level (neglecting refraction) the visible horizon would be about 36 km away and only 0.32° below the true horizontal, even at 1,000 m elevation the horizon is only 1.0° below. Refraction usually (not always)  decreases this dip a little more.

Of course this is all for the globe, I can't help you on the the flat earth other than to say what I would expect to happen.

I meant to get this posted earlier, but it didn't happen. Little things like eating and digging the garden etc butted in.

[TotesNotReptilian]

FYI, the equation I gave above,

d = R cos^-1(R/(R+h))

calculates the ground distance to the horizon (the arc length of SG in rabinoz's picture). That's why it looks different from his equation. However, they are approximately the same when h << R, which is why the approximate equation is the same.