If you transform a sphere into a plane or vice versa, points on the plane will be different distances, per Gauss. If you can make a flat map with constant scale, the earth is flat. If you can make a spherical map with accurate distance, direction, and scale, the earth is not flat, or Gauss' theorem is not true. There is no flexible measuring in geometry, the ruler is straight and constant. If you need to bend or stretch the ruler, you are proving Gauss' point.
When you flatten the globe into a disk as in the FAQ map, mathematically each latitude gets longer all the way to the south pole. Do car odometers in Australia measure distance differently from those in EU? Planes fly faster and have longer range? Do rulers stretch as they travel south?
I believe everything works because of the distance metric changing. My guess is that the changes to the distance metric nullify the changes in shape and i believe i can make a compelling case for this.
- The distance metric on a globe is haversine. This is a function that takes lat/long as input. lat/long are invariant on the AE map, and so the AE map with haversine as a distance metric will return the same distance between any 2 points on the map as a globe does. The formula to calculate angles on a globe is also expressed in function of lat/long coordinates and is again invariant under AE. So in these 2 maps, all distances and all angles are the same as on the globe.
As gauss measures curvature based on distances, i really can't see how the curvature can change.
- I thought about simulating distances in my little simulation, and didn't because it's pointless. I would be doing haversine in both cases on the same numbers...
- The bug-looping-a-circle-method to find curvature (if it's less than 2*π*R, also gives the same result in my world)
- and finally a proof by construction: construction of the flat world happens in 2 phases: transform to celestial coords(lat, long, dist) and then draw the latitude on a linear axis instead of a radial one (like AE). I do not believe the drawing on a different axis can cause curvature to break. This drawing is just a rendering of the results. The coordinates don't change. Math can't see how i draw things.
However i believe the switch to celestial coordinates might be the problem. When we switch from cartesian to celestial coordinates, all coordinates change, and the distance formula breaks. That is why we switch the distance to haversine at this point. If we draw a sphere in cartesian coordinates, and then express it in celestial coordinates, while changing the distance metric, the sphere is still a sphere. If we only changed the coordinates without changing the distance function, gaussian curvature would probably break.
So i believe gaussian curvature is dependent on shape and distance. If we change the shape and compensate with the distance, this works. Of course in reality this also works. People have been using haversine to calculate spherical distances for a very long time, and if the sphere would cease to be when you transform from cartesian to celestial, that would be rather problematic.
Bending the light is, as the EA page in the FAQ says, "unknown forces with unknown equations". Making the ruler curved and the scale adjustable by location is fudge factor without any justification, what psychologists call "motivated reasoning". You get there by observing that assuming FE produces bad results, so you hypothesize fudge factor without proof in order to save your belief.
Why does light travel straight on the globe? (Because it matches observations?) Same with bendy light. Again, it's the globe model transformed. The explanation is the same. As for "motivated reasoning", can you give me the reason why only an orthonormal basis may be considered to describe the universe?
Your model shows how we could see sunset/sunrise and day/night on FE, assuming some directional phenomenon and the unexplained bending of light, coincidentally exactly the equations to transform RE into FE. But you're not done with explaining all phenomena we observe, we all see the dome, geometrically we all see all of it. Yet at the same moment, some see stars all over the dome, others see light blue all over the dome, they can be as close as perhaps 300 miles. Someone in the northern Hemisphere sees completely different stars than southern hemisphere.
It works the same way as in the globe model, but then transformed. If you'd like to get a visual, draw the scene on the globe, draw light-rays, transform. If the globe can explain it, so can we.
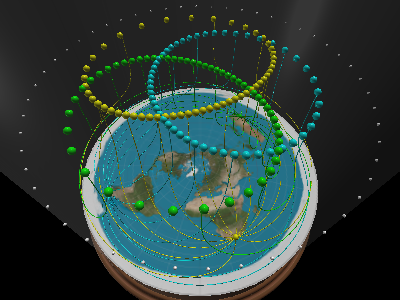
Then there is Sigma Octatis, the southern (pretty close) pole star. At the summer (northern hemisphere) equinox, at midnight in South Africa it is just after sunset in western Australia and just before sunrise in South America. You can see Sigma Octatis directly south from all these places at that time. On FE disk map, Sigma Octatis is in directly opposite directions from South America and Australia.
So please show the dome appearance in your model. I will be interested to see: Where is Sigma Octatis and how do the light rays from it travel? How does the dome appear light blue for some, and for those who see it as dark, different stars. How do those stars appear to travel across the dome in different directions at the same time? Please show with your model.
Same answer as above. If it works on a globe, it works on the flat earth as it is the globe model transformed. I will not be rendering out all examples you've requested. We believe this model is only of philosophical use and thus quite pointless to do so. But i've explained all formulas, feel free to investigate further. However i have rendered the south star before. Couple of notes on the picture: All points below the southpole are transformed into a circle (thank you AE map). So the yellow circle you see is the star. The colored lines are the sightlines from the 3 observers. It's easy, draw on a globe, add lightrays from source to destination, transform. The other pictures show from where the southstar is visible and the shared area of the sky the 3 observers can see (it's the area inside the yellow circle and outside the colored ones). I hope it makes sense

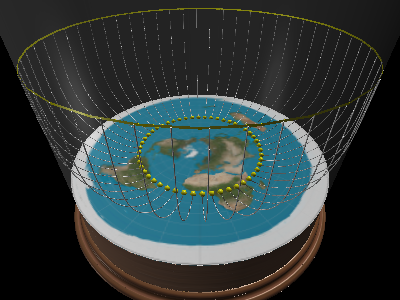
Do you agree that flattening a sphere into a disk will geometrically distort the distances? Or is Gauss' theorem not true?
I believe distances only become distorted depending on the distance metric. Haversine is valid for both models, but generally, all formulas need to be coord transformed (as one typically does in physics when doing coord transforms...)